反函数的求导法则
反函数的求导法则fanhanshu de qiudao faze
设函数x=φ (y)在点y的某一邻域内连续且严格单调,又在点y处导数φ ′ (y)存在且不为零,则它的反函数y=f (x) 在对应点x处可导,并且f′ (x) =1 / φ ′ (y)。
例 求 (arcsinx)′。
解 由于y=arcsinx的反函数x=siny在区间 (-π/2,π/2)内严格单调、可导,且(siny)′ = cosy> 0,根据反函数的求导法则可知,x=siny的反函数y = arcsinx在对应区间 (-1,1)内可导,且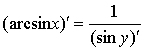
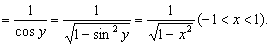
☚ 导数的四则运算法则 复合函数的求导法则 ☛
- 颅狭窄症是什么意思
- 颅痛定是什么意思
- 颅的内面是什么意思
- 颅的外面是什么意思
- 颅的年龄性变化及性别差异是什么意思
- 颅盖是什么意思
- 颅相学是什么意思
- 颅相学犯罪观是什么意思
- 颅相重合是什么意思
- 颅相重合法是什么意思
- 颅神经损伤是什么意思
- 颅窝是什么意思
- 颅结合是什么意思
- 颅缝是什么意思
- 颅缝和颅囟影是什么意思
- 颅缝早闭是什么意思
- 颅缝早闭综合征是什么意思
- 颅缝骨化症是什么意思
- 颅胀是什么意思
- 颅脑ct检查是什么意思
- 颅脑x线摄影机是什么意思
- 颅脑x线检查是什么意思
- 颅脑伤是什么意思
- 颅脑先天发育畸形是什么意思
- 颅脑创伤是什么意思
- 颅脑和脊髓肿瘤x线诊断是什么意思
- 颅脑外伤伴发的精神障碍是什么意思
- 颅脑外伤伴发精神障碍司法鉴定是什么意思
- 颅脑外伤精神障碍是什么意思
- 颅脑外科临床解剖学是什么意思
- 颅脑影像诊断学是什么意思
- 颅脑战伤是什么意思
- 颅脑战伤异物是什么意思
- 颅脑战伤癫痫是什么意思
- 颅脑战伤综合征是什么意思
- 颅脑战伤脑脊液漏是什么意思
- 颅脑战伤脑脓肿是什么意思
- 颅脑战伤脑膨出是什么意思
- 颅脑战伤颅内血肿是什么意思
- 颅脑战伤颅骨缺损是什么意思
- 颅脑手术针刺麻醉是什么意思
- 颅脑损伤是什么意思
- 颅脑损伤后低颅压征群是什么意思
- 颅脑损伤护理是什么意思
- 颅脑损伤的处理是什么意思
- 颅脑损伤的眼部表现是什么意思
- 颅脑放射复合伤是什么意思
- 颅脑断面扫描是什么意思
- 颅脑特殊类型战伤是什么意思
- 颅脑疾病影像诊断图谱是什么意思
- 颅脑研究中心是什么意思
- 颅脑计算体层摄影是什么意思
- 颅脑超声波是什么意思
- 颅脑颈部应用解剖彩色图谱是什么意思
- 颅腔是什么意思
- 颅裂是什么意思
- 颅针疗法是什么意思
- 颅钻是什么意思
- 颅面外科是什么意思
- 颅面的演化是什么意思