自回归条件异方差autoregression conditional heteroscedasticity

考虑线性或非线性模型y_t＝f(x_t,β)+ε_t，其中y_t是被解释变量，x_t是解释变量，β是模型的参数。
传统的计量经济理论都假定条件方差V(ε_t|ε_t-1)与ε_t-1无关。但有些经济变量像通货膨胀，汇率和股票价格在较大幅度的波动后面一般紧接着较大幅度波动，较小幅度的波动后面一般连着较小幅度的波动。ARCH方法比传统方法更适合于对这些变量建立模型，它仍假定无条件方差V(ε_t)=σ²为常量，但条件方差V(ε_t|ε_t-1)依赖于ε_t-1，因而符合这些变量的波动特征。
ε_t＝y_t-f(x_t,β)是一个实数域上的离散时间随机过程，ψ_t是直到t时间的所有信息集(即由ε₁，…，ε_t产生的σ-域)。ARCH(q)过程由下面给出：

其中q>0;α₀>0,α_i≥0,i=1，…，q;
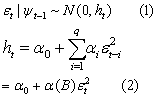
当且仅当α(1)<1时，由(1)和(2)定义的ARCH(q)过程是宽平稳的，其均值E(ε_t)=0，无条件方差V(ε_t)=α₀(1-α(1))^-1且协方差cov(ε_t,ε_s)=0,t≠s。
设样本有N个观察个数，则模型估计的对数似然函数为：

使该函数达最大值，就可得到参数β,α的估计。
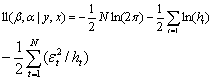
可采取由Engle(1982)提出的拉格朗日乘子检验(Lagrange multiplier test)对ε_t是否有ARCH现象进行检验，首先，对ε_t平方，得到ε_t²。然后，对ε_t²进行AR(q)自回归估计得到拟合优度R²。最后，利用结果：在不存在ARCH的原假设下，统计量NR²服从于自由度为q的χ²分布。若显著性水平为5%，当NR²值大于χ²分布的临界值时，则拒绝ε_t不存在ARCH的假设，即认为存在ARCH现象。