阶的估计方法

---

数论与函数论的重要方法，它在本质上属于极限的方法。

阶的估计方法包括各种和式的估计法。例如，分部求和法、欧拉求和法、泰勒展开及各种渐近展开、母函数方法、拉普拉斯方法、验相法、最速下降法以及陶贝尔方法等等。

运用这种方法，可以卓有成效地处理各种复杂的数学问题，简化计算程序，得到精密的结果。阶的估计方法所研究的主要对象是各种形式的变量，特别是无穷大量与无穷小量，以下简称为无穷量。由于无穷量的定义只刻划变量的变化趋势，要描述它们的快慢就需要动的概念。

若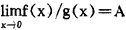，．当A=0时，称x→a时，f(x)相对g(x)是一个无穷小量，特别当f(x)与g(x)都是无穷大量时，称f(x)是比g(x)低阶的无穷大量或g(x)比f(x)为高阶的无穷大量，f(x)与g(x)都是无穷小量时，称f(x)是比g(x)高阶的无穷小量；当A≠0时，称f(x)与g(x)是同阶的，特别当A=1时，称f(x)与g(x)是等价的。在x→a时，往往将无穷小量(x－a)^α，(α＞0)作为基本无穷小量，并用它去度量其它的无穷小量。在x→a，凡是与(x－a)^α，(α＞0)同阶的无穷小量其趋于0的快慢都是一个等级的，可用数α来反映，并称它们都是α阶的无穷小量，在理论与实际中所遇到的无穷量往往比较复杂，并且在许多问题中对一个函数的精确性状的要求不是很高，而只要对其阶作出符合要求的估计就可以了。

但要对变量的阶进行估计，就需要一个重要的符号：大“0”或“《”。

设D是一个实数集，f(x)是定义在D上的复值函数，φ(x)是在D上的正值函数，若存在一个与x无关的正常数A，使得｜f(x)｜≤Aφ(x)在D上恒成立，则称φ(x)在集D上是f(x)的优函数或强函数，并记为f(x)=0(φ(x))或f(x)《φ(x)，(x∈D)。

显然这两个符号是不等式的缩写，它表明了｜f(x)｜在D上的数量阶不超过φ(x)的阶。特别当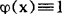时，这两个符号表明｜f(x)｜在D上有界，例如，sinx=0(1)或sinx《1，(－∞＜x＜+∞)；logx=0(x^α)(α＞0)或logx《x^α，(x≥1)；x^α=0(e^x)或x^α《e^x，(x≥1)等等。

利用阶的估计方法可以得到许多重要函数的渐近公式，例如，对加马函数，有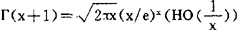，即著名的斯特林公式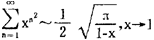；；对n阶贝塞尔函数，则有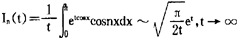等等。