欧拉方程
欧拉方程Euler equation
是解变分问题的一个基本工具,它给出泛函极值存在的一阶必要条件。
设J(y)是定义于某集D上的一个泛函,D含于某个函数空间y。对给定y∈D,若对任何h∈y,导数:
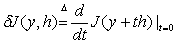
h→δJ(y,h)
为J在y的变分,记作δJ(y)。若J(y)在某点y*∈D取得极值且变分存在,则必定δJ(y*)=0,即y=y*满足方程:
δJ(y)=0 (*)
在很多具体问题中,泛函J(y)通常表为某个积分,而欧拉方程则可转化为一个微分方程。例如,设
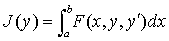
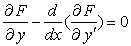
☚ 最优控制理论 新古典派总体增长模型 ☛
- 赫德森, 曼利·奥特默是什么意思
- 赫德,r.d.h.是什么意思
- 赫怒是什么意思
- 赫恩小体是什么意思
- 赫恩滋小体是什么意思
- 赫恩登, 威廉·亨利是什么意思
- 赫恩,r.l.是什么意思
- 赫恩,拉夫卡迪奥是什么意思
- 赫戈木是什么意思
- 赫戏是什么意思
- 赫戲是什么意思
- 赫拉是什么意思
- 赫拉克利亚之战是什么意思
- 赫拉克利亚庞提卡之战是什么意思
- 赫拉克利亚普罗庞提斯之战是什么意思
- 赫拉克利特是什么意思
- 赫拉克利特——一切事物都在发展是什么意思
- 赫拉克利特的辩证法是什么意思
- 赫拉克利特论正义与善恶是什么意思
- 赫拉克勒斯是什么意思
- 赫拉克勒斯 [古希腊]佚名是什么意思
- 赫拉克勒斯和恶狗凯耳柏洛斯是什么意思
- 赫拉克里亚是什么意思
- 赫拉 [古希腊]佚名是什么意思
- 赫拉尔多·迪埃戈是什么意思
- 赫拉斯是什么意思
- 赫拉波利斯是什么意思
- 赫拉特是什么意思
- 赫拉特之战是什么意思
- 赫拉班是什么意思
- 赫拉细胞是什么意思
- 赫斐斯塔司是什么意思
- 赫斤是什么意思
- 赫斯是什么意思
- 赫斯之威是什么意思
- 赫斯之怒是什么意思
- 赫斯伯格是什么意思
- 赫斯佩勒是什么意思
- 赫斯佩里德斯是什么意思
- 赫斯基亚特人是什么意思
- 赫斯塔特银行危机事件是什么意思
- 赫斯怒是什么意思
- 赫斯特是什么意思
- 赫斯特孟骚是什么意思
- 赫斯特征是什么意思
- 赫斯特报团是什么意思
- 赫斯特报系是什么意思
- 赫斯特新闻社(美)是什么意思
- 赫斯特蒙苏是什么意思
- 赫斯特,w.h.是什么意思
- 赫斯特,威廉·伦道夫是什么意思
- 赫斯科维茨是什么意思
- 赫日是什么意思
- 赫昈昈是什么意思
- 赫明堂是什么意思
- 赫显是什么意思
- 赫晔是什么意思
- 赫晞是什么意思
- 赫-普综合征是什么意思
- 赫曦是什么意思