概念的定义gainian de dingyi

揭示概念内涵的逻辑方法.例如：“含未知量的等式叫做方程.”定义是由被定义项、定义项和定义联项三部分构成的. 上例中“方程”是被定义项，“含未知量的等式”是定义项，“叫做”是定义联项.因为概念反映着事物的特有属性，又是语词的思想内容，因此，要给概念下定义，既可以从揭示概念所反映的特有属性方面进行，也可以从揭示语词的涵义方面进行.这就分别形成了真实定义和语词定义.在真实定义中，最常用的一种下定义方法，就是通过揭示被定义概念的最邻近的属和种差下定义.上述给“方程”下定义就用的是这种方法.语词定义就是用说明或规定语词的意义的方法给概念下定义.
在中学数学中，用“最邻近的属和种差”下定义的方法常有以下几种特殊形式：
❶发生定义的方式，是用对象的发生或形成（构造）过程作种差的下定义方式.例如：“圆就是由一线段的一端点在平面上绕另一端不动点运动而成的一条封闭曲线”.
❷关系定义方式，是以对象间的关系及其特点作为种差的下定义方式.例如：“偶数就是能被2整除的整数”.归纳定义方式是关系定义方式的特殊情形，如由给定的数列的初项和接邻项的关系式，可顺次确定出它的各项至第n项，从而定义出一个数列.其中接邻项的关系式叫做递推式.例如，用归纳定义方式作出的“斐波那契数列”的定义：

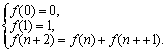
下定义的规则有：
❶定义项的外延与被定义项的处延必须是全同的.
❷定义项中不能直接地或间接地包括被定义项.
❸定义只要能是肯定的，就不应当是否定的.
❹定义项中不能包括含混的概念和语词.
❺定义是不能循环的.