7.5.1 偏导数
设z=f(x,y),则
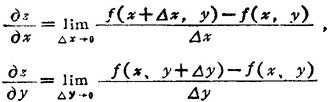
分别称为函数z=f(x,y),关于x、y的偏导数。其求法可按单变量函数微分法则求出,只须将其余变量看作常数。其定义可推广到多变量函数。
7.5.2 偏微分、可微函数、全微分
多变量函数对其中一个变量的偏微分为
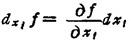
若函数u=f(x,y)的全设变量可写为
△u=f(x+△x,y+△y)-f(x,y)=A△x+B△y+0Cρ)
式中A,B与△x,△y无关。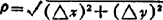 ,则称函数u=f(x、y)在点(x、y)可微分,且偏导数
,则称函数u=f(x、y)在点(x、y)可微分,且偏导数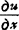 ,
,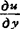 一定存在,而且
一定存在,而且
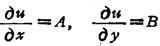
设变量的线性主部
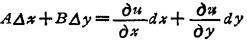
称为函数u=f(x,y)的全微分,记作
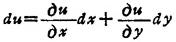
以上定义可以推广到u=f(x1,x2,x2,…xn)的一般形式。
7.5.3 复合函数微分法
设g=f(u,v,…,ω),而u,v,…,ω都是x,y,…,t的函数,则
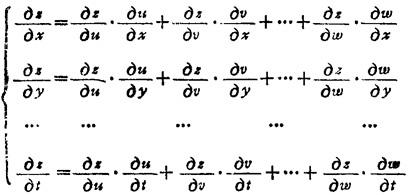
7.5.4 混合偏导数的性质
若混合偏导数连续,则与微分的顺序无关。例如:
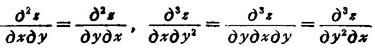
- 窦秉钧是什么意思
- 窦穆矫太后诏旨案是什么意思
- 窦空子是什么意思
- 窦窌是什么意思
- 窦窖是什么意思
- 窦窿是什么意思
- 窦立勋是什么意思
- 窦纳乐是什么意思
- 窦维鍌是什么意思
- 窦群是什么意思
- 窦联芳是什么意思
- 窦胄卿诗集是什么意思
- 窦腔造影是什么意思
- 窦臮是什么意思
- 窦舜卿是什么意思
- 窦良茂是什么意思
- 窦苹是什么意思
- 窦茂是什么意思
- 窦荣定是什么意思
- 窦蒙是什么意思
- 窦薛裕是什么意思
- 窦融是什么意思
- 窦融传是什么意思
- 窦融受累世之封,吴芮袭传家之庆。愚者暗于成事,智者见于未萌。是什么意思
- 窦融表已来关右,陶侃军宜次石头。是什么意思
- 窦行冲是什么意思
- 窦诞是什么意思
- 窦诞与襄阳公主合葬墓是什么意思
- 窦诞墓志是什么意思
- 窦贞固是什么意思
- 窦车骑是什么意思
- 窦轨是什么意思
- 窦轨击鼓败稽胡是什么意思
- 窦道是什么意思
- 窦遵是什么意思
- 窦锦是什么意思
- 窦镇是什么意思
- 窦闺织妇惭诗句,南国佳人怨锦衾。是什么意思
- 窦雅是什么意思
- 窦靖童就是王菲和窦唯的升级版是什么意思
- 窦靖童:不安之乐是什么意思
- 窦静是什么意思
- 窦静庵遗书是什么意思
- 窦马村是什么意思
- 窦马遗址是什么意思
- 窦默是什么意思
- 窦默谏为臣当直案是什么意思
- 窧是什么意思
- 窨是什么意思
- 窨下的是什么意思
- 窨下酒是什么意思
- 窨井是什么意思
- 窨井等地下设施致人损害的责任是什么意思
- 窨付是什么意思
- 窨偧是什么意思
- 窨凉踱踱是什么意思
- 窨口是什么意思
- 窨子是什么意思
- 窨子屋是什么意思
- 窨子房是什么意思