圆锥曲线

---

亦称“二次曲线”。

是用一平面去截正圆锥面时所产生的交线。设圆锥为正圆锥，α(0＜α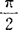＜)为母线与锥轴的交角，M为不通过锥顶的截面，β(0≤β≤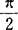)为M与锥轴z的交角，则当α≤β≤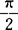、β=α、0≤β＜α时，其交线分别称为椭圆、抛物线、双曲线(见图15)。

关于圆锥曲线的研究，早在古希腊就取得了初步成果。公元前4世纪，希腊的门内玛斯(Menaechmns)圆锥曲线图曾用垂直于圆锥一母线的平面去截顶角为锐角、直角、钝角的圆锥面，将分别得到的交线称为“锐角曲线”、“直角曲线”、“钝角曲线”。

这三种曲线就是后来的“椭圆”、“抛物线”、“双曲线”。后来，欧几里得、阿基米德等也对圆锥曲线进行过研究。

而阿波罗尼斯(Apllonius)则是集前人之大成者，他对圆锥曲线进行了系统的研究，取得了显著成果，发表了巨著《圆锥曲线论》(共8卷)。在这部著作中，他明确指出，只要改变截平面与圆锥母线的夹角，三种圆锥曲线都可以由同一个圆锥体截取而得。

但这些研究基本上停留在抽象的理论探讨上，缺乏实践基础，故发展缓慢。到17世纪，随生产和科学的发展，圆锥曲线在实践中找到了现实原型。如刻卜勒发现太阳系行星的轨道是椭圆，有些彗星的轨道是双曲线；伽利略发现抛射体的轨道是抛物线等。

17世纪上半叶，笛卡儿发表了《几何学》，引进了“复数”，制定了解析几何。

恩格斯说：“数学中的转折点是笛卡儿的复数。有了复数，运动进入了数学，有了复数，辩证法进入了数学……”(《自然辩证论》第236页)。

在解析几何中，用动点轨迹来建立圆锥曲线的概念：在平面上，若一动点到两定点的距离之和为定长时，则该动点的轨迹称为椭圆；若一动点到某定点和到某定直线的距离相等时，则该动点的轨迹称为抛物线；若一动点到两定点的距离之差是常数时，则该动点的轨迹称为双曲线。

这三种曲线，在一定条件下可以相互转化。

从原来用相对静止的观点，把圆锥曲线看成是截割正圆锥面所得交线，到用运动的观点，将圆锥曲线视为点的轨迹，这是人们在对圆锥曲线认识上的一次飞跃。圆锥曲线理论在光学、建筑、航海、工程和人造卫星等领域，得到了广泛的应用。