非参数密度估计

---

在非参数统计模型中，假定总体分布是完全未知，即不能通过有限个参数加以界定，而且分布的泛函形式也是未知，通常可用分布函数或密度来描述其分布。

但当样本为多维时，更方便地是使用密度函数。无论从统计模型的设定、解释或是统计推断，都同估计未知分布密度有关。

密度估计的非参数方法的重要进展，始于Rosenblatt(1956)的工作，而Parzen(1962)的工作则将一项重要的估计方法即核方法系统化。

另一项值得一提的工作，则是Loftsgarden和Quesenberry(1965)完成的。

他们提出了密度估计的另一种方法，即最近邻估计法，然而对最近邻估计的系统研究则是Wagner(1973)、Devroye和Wagner(1977)完成的。至此已形成非参数密度估计的两个主要方法。

Parzen的核估计是：假设Z₁，…，Z_n是一组来自未知密度函数f(x)的(d≥1)维样本。设定一个定义在R^d上核函数K(·)［通常假定K(·)也是密度，例如正态密度等］及一串常数h_n＞0。定义基于Z1，…Zn的以K(·)为核的f(x)的估计为

并称hn为窗宽，它是核估计的主要光滑参数。随后为了理论分析的方便，也有作者将核K的限制放宽，不要求K非负。

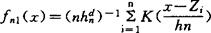
最近邻估计则是基于直观观察：在样本Z₁，…Z_n中，对估计函数值f(x)来说，其作用最大的是“最接近”x的那些样本，具体来说，对给定正整数k=kn(≤n)，令an(x)为中心在x的R^d中的球的半径，使该球含Z₁，…，Z_n中的k_n个样本点，记此球的体积为S_n(x)，则定义f(x)的最近邻估计为

f_n2(x)=kn／nSn(x)

在这段时间，也有人考虑这两种方法的结合，即随机窗宽核估计，见Moore和Yackel(1977)的工作。

到现在为止，文献中出现的非参数密度估计的方法已很多，较为系统的总结可见P．B．Rao(1983)的专著。

其主要成果如下：(1)估计的相合性。Parzen在他的著名工作中得到如下结果，对核K及窗宽的适当限制下，估计量是逐点均方相合及一致相合的，即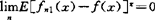及。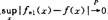

而Devroye(1980)则在很一般条件下，得到估计量的一致强相合性(即。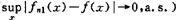

对于最近邻估计，Devroye和Wagner(1977)在很弱的假定下，证明了一致强相合性。

(2)收敛速度。Schuster(1976)证明：对导数有界的密度族，核估计有强一致收敛速度。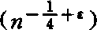

陈希孺(1983)则将此结果改进为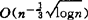，并指出其主要部分的指数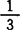已不能再改进。对于最近邻估计，陈希孺(1981)证明：对r阶导数存在的密度族，逐点收敛速度为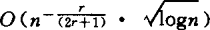，而达不到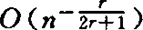；陈希孺(1983)还对满足Lipshitz条件的密度族，证明了其一致收敛速度为。

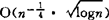(3)一致相合的必要条件。这是Schuster(1969)首先提出的一个问题，即对核K及窗宽满足一定条件，由此构造的核估计若一致收敛于某个函数g，问g是否必为总体密度，且g是否必须一致连续?Schuster在对K及hn的一系列假定下，得到了肯定的回答。

陈希孺、成平先后对之作了彻底改进。关于最近邻估计相合的必要条件，其问题的提法同前。

一维(即d=1)的情形是由陈希孺、柴根象得到肯定的回答。(4)L₁模相合性。L₁模，即∫｜f_n(x)－f(x)｜dx，其中f_n或为．f_n1或为f_n2，也可是任一别的密度估计。它是估计偏差的更为自然的一个整体测度。

其相合性研究对模式识别、判别分析均有重要应用。Devroye(1983)在很为一般假定下证明L₁模相合与L₁模强相合、均方相合等结果，且给出相合的充要条件。

以上这些成果全在大样本理论方面。事实上由于非参数模型的特点，不可能有太多的深入的小样本结果。

关于后者，在文献中主要是涉及无偏密度估计的存在性。B．P．Rao在其专著中对此也有提及。此外，对于大样本方面的成果即使从面上也有许多重要成果未在此提及的，例如密度导数的估计，陈桂景(1984)有系统的成果。

近几年，密度估计的文章仍在文献中不时出现。

主要是：

(1)L_r模及平均L_r模相合性。其定义分别是m_r(fn)=∫｜f_n(x)－f(x)｜^rdx及M_r(f_n)=E(m_r(f_n))，r≥1，f_n是任一密度估计。考虑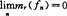，a．s．或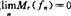成立的充要条件。这是对Devroye(1983)工作的深化。

当f_n为核估计时，白志东和赵林城(1987)证明：如K为密度，则充要条件是

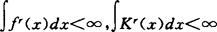
以及

，。

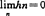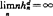当f_n为最近邻估计时，必须限定r＞1。赵林城(1986)在d=1时，吴跃华(1989)对一般的d，证明：如果

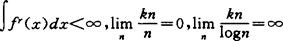
则

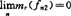，a．s．

(2)研究随机直方图估计。这是对通常的直方图估计的一个本质改进。

这种估计由J．Chen和H．Rubin(1984)首先加以研究。

他们证明：在一系列复杂条件下，这种估计是L₁相合的。

陈希孺、赵林城(1987)则得到L₁强相合条件。而且，赵林城、Krishnaish、陈希孺(1987)很快又对此条件作了实质上改进，并建立了一般的L_r模相合性。

(3)研究密度估计的实施问题，其中特别是对核估计，研究有关参量的实际选择，引出了许多较为实用的方法。B．W．Silverman(1986)的专著“Density estimation for statistics and Data-analysis”对此有较详细的介绍，并且也提出了尚未解决的问题。

除了以上提到的3个主要发展方向外，还有一些研究新的估计方法的工作。另外密度估计的应用的研究也是一个重要趋势。

。【参考文献】：

1 Rosenblatt M. Ann Math Statist, 1956,27:832～837

2 Parzen E. Ann Math statise, 1962,33:1065～1076

3 Loftsgarden D O, et al. Ann Math Statist, 1965,36:1049～ 1051

4 Devroye L P. Ann statist,1977,5:536～540

5 Schuster EF. Ann Math statist, 1969,40:1187～1195

6 陈希孺．中国科学，1982，25：455～467

7 陈希孺．系统科学与数学，1983，3：263～272

8 Rao B．P．Nonparametric functional estimation，Academic press，1983

9 赵林城．应用概率与统计，1987，3：46～50

(同济大学柴根象教授撰)

上一篇：概率度量空间上的非线性分析
下一篇：现代科技综述大辞典上目录

"非参数模型非参数模型

---

信号检测论模型的一种。

用于测量感觉辨别力和反应偏向。即用接受者操作特征曲线(ROC)(如图)下的面积值来表达感觉辨别力(A′)和反应偏向(B″)。其中A′=0．5+［(H－FA)(1+HFA)］／［4H(1－FA)］，(H代表击中概率，FA代表虚报概率)。

A′的值在0～1之间波动，A′=0．5表示无辨别力。

B′_H或B″表示反应偏向，B′_H=1－［H(1－H)］／［FA(1－FA)］；B″=［H(1－H)－FA(1－FA)］／［H(1－H)+FA(1－FA)］。B′_H和B″均在－1～+1之间变化，0表示无反应偏向，正值表示标准宽松，负值表示标准严格。

应指出的是，A′与d′有高相关，且被广泛用于信号检测的研究。