刚体是一种特殊的质点组,其中任何两质点间的相对位置不因外力的作用而发生改变,和质点一样这是从实际中抽象出来的一种理想模型,在实际问题中,当物体的大小和形状在运动过程中的变化可忽略不计时,就可近似地作为刚体来处理。
设刚体在t时刻的瞬时平动速度及角速度分别为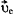 及
及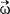 ,则刚体上任一点i的瞬时速度可写出为
,则刚体上任一点i的瞬时速度可写出为
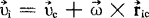
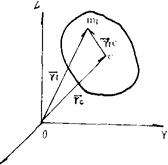
式中ric为i点相对于质心的矢径。因此刚体对某定点0的动量矩可写成
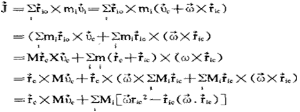
此式中M是刚体总质量。上式第二大次表示刚体绕质心的动量矩,若以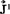 示之,并以(xi,yi,zi)示
示之,并以(xi,yi,zi)示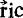 的分量,则可得
的分量,则可得
J’x=Ixxωx-IxYωY-Ixzωz
J’Y=-IYxωx+IYYωY-IYzωz
J’z=-Izxωx-IZYωY+IZzωz
式中
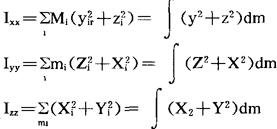
Ixx、Iyy及Izz为刚体绕X轴、Y轴及E轴的转动惯量。
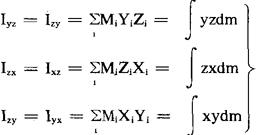
统称为惯量积
若引入(定义)惯量张量
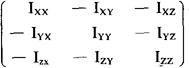
则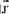 的分量式可简单地表示为
的分量式可简单地表示为
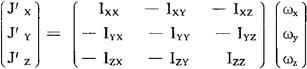
类似地,刚体的动能可写出为
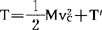
式中T′为刚体相对于质心的动能。
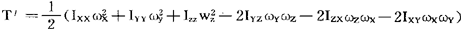
- 先天性胆总管囊状扩张是什么意思
- 先天性胆总管囊肿是什么意思
- 先天性胆管囊状扩张症是什么意思
- 先天性胆管扩张症是什么意思
- 先天性胆管扩张症是什么意思
- 先天性胆管闭锁是什么意思
- 先天性胆道闭锁是什么意思
- 先天性胆道闭锁是什么意思
- 先天性胫骨假关节是什么意思
- 先天性胰腺疾病是什么意思
- 先天性胸腺发育不全是什么意思
- 先天性胸腺发育不良是什么意思
- 先天性脊柱侧凸是什么意思
- 先天性脊柱后凸畸形是什么意思
- 先天性脑积水是什么意思
- 先天性膀胱颈部梗阻是什么意思
- 先天性膈疝是什么意思
- 先天性膈疝是什么意思
- 先天性膈疝是什么意思
- 先天性输尿管异位开口是什么意思
- 先天性输尿管狭窄是什么意思
- 先天性鞘膜积液是什么意思
- 先天性风疹是什么意思
- 先天性食管狭窄是什么意思
- 先天性食管闭锁是什么意思
- 先天性食管闭锁及气管食管瘘是什么意思
- 先天性食管闭锁及食管气管瘘是什么意思
- 先天性马蹄内翻足是什么意思
- 先天性马蹄内翻足是什么意思
- 先天性马蹄内翻足是什么意思
- 先天性马蹄内翻足是什么意思
- 先天性髋关节脱位是什么意思
- 先天性髋关节脱位是什么意思
- 先天性髋关节脱位是什么意思
- 先天性髋关节脱位是什么意思
- 先天性髋关节脱位是什么意思
- 先天性髋关节脱位是什么意思
- 先天性髋内翻是什么意思
- 先天性高肩胛症是什么意思
- 先天性高肩胛骨是什么意思
- 先天愚型是什么意思
- 先天直观形式是什么意思
- 先天知性形式是什么意思
- 先天综合判断是什么意思
- 先张法施工工艺是什么意思
- 先张法施工工艺是什么意思
- 先征后返优惠政策是什么意思
- 先意①承欲②者,谄也;繁称③文辞者,博也;策选④进谋者,权也;纵舍⑤不疑者,决也;先分⑥不足以窒非⑦者,反也。是什么意思
- 先意①承欲②者,谄也;繁称③文辞者,博也;策选④进谋者,权也;纵舍⑤不疑者,决也;先分⑥不足以窒非⑦者,反也。是什么意思
- 先施百货公司是什么意思
- 先是……接着……是什么意思
- 先是……跟着……是什么意思
- 先是……随着(随即、随后)……是什么意思
- 先秦、两汉文学是什么意思
- 先秦两汉诗精华是什么意思
- 先秦民族史和诸国史是什么意思
- 先秦经济史是什么意思
- 先进典型材料是什么意思
- 先进典型的宣传是什么意思
- 先进典型示范法是什么意思