斐波那契数
斐波那契数feibonaqishu
1225年在意大利比萨市进行的一次竞技比赛上，有人向当时的著名数学家斐波那契提出了一个问题：求一个数的完全平方，它加5后仍然是完全平方数，减5后也是完全平方数.斐波那契找到了这个问题的一个答案： (41/12)2—5=(31/12)2,(41/12)2+5=(49/12)2.把这个问题一般化，即若三个数(x/y)2-z,(x/y)2,(x/y)2+z是确定的完全平方，这样的三个数称为斐波那契数.也有人把斐波那契数列的项，叫斐波那契数(见“斐波那契数列”). 实际上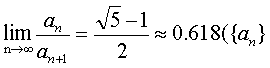
| 是斐波那契数 |
☚ 斐波那契数列 等差数列 ☛
- :-’|是什么意思
- :’-(是什么意思
- :’-)是什么意思
- ’-)是什么意思
- ’90山西企业经营者荟萃是什么意思
- ’92乌鲁木齐边境地方经济贸易洽谈会是什么意思
- ’93专利技术、新产品乌鲁木齐博览会是什么意思
- ’93全国适用技术成果信息新疆巡回发布会是什么意思
- ’94全国发明与专利博览会暨百强县与新疆交流协作会是什么意思
- ’94新疆国际太阳能应用技术研讨会是什么意思
- ’95“中国环游丝绸之路”国际公路自行车邀请赛是什么意思
- ’95广角是什么意思
- ’95湘中是什么意思
- ’96“中国环游丝绸之路”国际公路自行车比赛是什么意思
- ’96“大卫杯”全国马术锦标赛是什么意思
- ’97“中国环游丝绸之路”国际公路自行车邀请赛是什么意思
- ’97乌鲁木齐青少年天文知识竞赛是什么意思
- ’97天文冬令营是什么意思
- ’97新疆农村适用技术成果巡回展示会是什么意思
- ’97新疆青少年计算机奥林匹克竞赛是什么意思
- ’97马术障碍精英赛暨“澳门赛马会杯”大奖赛乌鲁木齐分区赛是什么意思
- ’98“‘吐乌大’高等级公路”杯国际足球友谊赛是什么意思
- ’98“中国丝绸之路”国际公路自行车赛暨全国公路自行车冠军赛是什么意思
- ’98新疆“桑塔纳”杯国际青年足球邀请赛是什么意思
- ’98新疆“热力杯”国际男篮邀请赛是什么意思
- ’99乌鲁木齐“农行杯”全国马拉松锦标赛暨国际马拉松比赛是什么意思
- ’99可口可乐u-21全国青年足球联赛（新疆赛区）是什么意思
- ’99新疆—芬兰施工机械研讨会是什么意思
- ’a是什么意思
- ’a’是什么意思
- ’bout是什么意思
- ’casion是什么意思
- ’cause是什么意思
- ’cern是什么意思
- :’d是什么意思
- ’ermite是什么意思
- ’fore prep.是什么意思
- ’gainst是什么意思
- ’gan是什么意思
- :-’i是什么意思
- ’ield是什么意思
- ’ild是什么意思
- ’mong是什么意思
- ’mongst是什么意思
- ’nah是什么意思
- ’nih是什么意思
- ’niu是什么意思
- ’nua是什么意思
- ’nuai是什么意思
- ’pear是什么意思
- ’sblood是什么意思
- ’s gravenhage是什么意思
- ’s hertogenbosch(或 den bosch)是什么意思
- ’slight:是什么意思
- ’tame是什么意思
- ’tide是什么意思
- ’tis:是什么意思
- ’twixt是什么意思
- ’ud’s:是什么意思
- ’um是什么意思