二项分布

一种离散型随机变量的分布。设在一次试验中事件A出现的概率为p(0

P(X=k)=p^k(1-p)^n-k,　k=0,1,2，…，n

则称X的分布是参数为n,p的二项分布，记为X~b(n,p)。常被应用于测验分数统计中。

二项分布binomial distribution

概率论中关于二项式n次乘幂的概率分布。描述随机现象的一种常用分布。整个总体中，仅有两种可能结果时，如种子的发芽与不发芽、产品的合格与不合格等，假定在一次抽样试验中，两种结果出现的概率分别为p和q，则p+q=1。在n次重复的试验中，则这两组出现次数不同的组合，构成如下的概率分布：

一般说来，只要每次试验结果发生某事件的概率为p，则独立地将此试验重复n次时，这个事件正好发生k次的概率就是P_n(k)。

因为正好是二项式(p+q)ⁿ的展开式中的一项，故名。

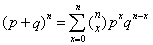
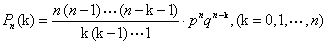
二项分布erxiangfenbu

指一种随机事件只有两种可能结果的概率分布。比如任选一个学生，只可能出现“男生”或“女生”这两种结果之一；完全凭猜测来回答一道正误题，只可能出现“做对”或“做错”这两种结果之一。设随机事件只有两种可能结果。一种可能结果的概率为p，另一种的概率为q(q=1-p)，如果这种随机事件出现n次，则下式的数学展开式的分布就称为二项分布：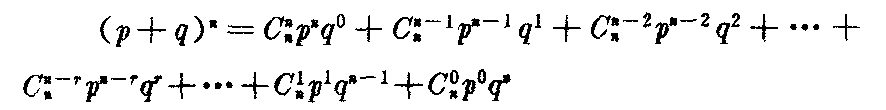

式中Cnn、Cnn-1、…是数学上的“组合”符号，其一般式为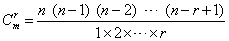

上式表示从n个元素中任取出r个元素来组合。当r=n或r=n-1时，则为Cnnn或Cnn-1。余类推。
据组合的关系式有Cn-rⁿ＝Crn(如Cnn-2=C2n)及任何数的0次幂均为1的原理，二项分布式可写成：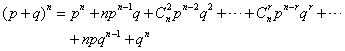

二项分布是一种离散型（即非连续型）的概率分布。当p=q=^1/2、且np≥5时，它近似于正态分布；当p≠q时，它为“偏态”分布，它的平均数和标准差分别为：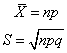

[例] 解10道正误题，学生全凭猜测作答的平均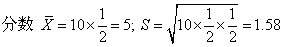

二项分布的优点是可以简捷地确定两种可能结果的各种概率。如在学生解10道正误题时，答对多少题才不是凭猜测而是凭自己真实知识得分呢？根据概率概念及二项分布公式有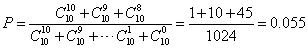

即考生凭猜测答对8题以上的概率约为5.5%，这几乎是一个小概率(通常5%以下称为小概率)，是不大可能出现的。故考生答对8题以上才认为不是凭猜测得分。由二项分布的对称性可知，考生答对2题以下也是不可能出现的小概率事件。

---

二项分布erxiang fenbu

在n重贝努利试验中，设每次试验某事件A出现的概率为p，令X是n次试验中事件A出现的次数，则X是一个离散型的随机变量，它的概率分布为

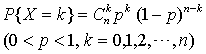
这个概率分布通常称为二项分布(因由二项式(p+q)ⁿ展开的各项组成).其中n,p为参数.当一个随机变量X的概率分布为二项分布时，称X服从参数为n,p的二项分布，记作X～B (n,p).

二项分布

一种常见的重要概率分布。在每次试验的条件相同的n次重复试验中，如果 一次试验发生某事件的概率为p，那么此事件发生k次的概率为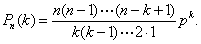(1-p)n-k(k=0,1，…，n)，这就是二项分布的具体表示式。

二项分布binomial distribution

是数理统计中离散分布之一，常用于描述随机现象。如小白鼠经γ射线照射后死亡概率为π，生存概率为1-π，则k个死亡，n—k个生存的概率为：

式中k=0,1,2，…n,0≤π≤1,π+(1-π)=1,n=正整数，均数为nπ。这一概率函数正好是二项式〔(1-π)+π〕ⁿ的展开式中的一项，故称二项分布。

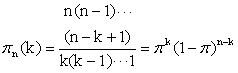
二项分布Binomial Distribution

亦称“重复n次的伯努里试验”。与其他各次试验结果无关，在每次试验中只有两种互相对立且独立的可能的结果，结果事件发生的概率在整个系列试验中保持不变的试验。用x表示随机试验的结果，若事件发生的概率是p，不发生的概率q=1-p，则n次独立重复试验中发生k次的概率是 p(x=k)=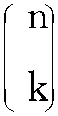 p^k(1-p)^n-k。

二项分布

二项分布是一种重要的离散型分布，由J.Bernoulli(1713)提出，故亦称Bernoulli分布，它在医学中常用于率的抽样研究，如总体率的估计及两样本率的比较等。概率函数及图形 设总体中的每一观察单位只具有相互对立的一种结果，如检查结果的阳性或阴性，动物的生存或死亡等；已知发生某一结果（如阳性）的概率为π，其对立结果的概率为(1-x)；各单位的观察结果相互独立。则从该总体中随机抽取n例，其中恰有X例是阳性的概率为下列二项式展开

含有πX的项，记作p(X)，称为二项分布的概率函数，即

式中，n为正整数，式(1)右端各项概率的总和为1

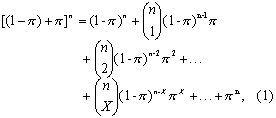
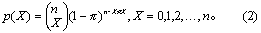
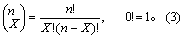
在含量为n的样本中，最多有X例为阳性的概率记作：

最少有X例为阳性的概率记作：

Q(X)有统计表可查，此处从略。
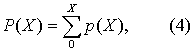
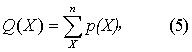
已知n与π，就能按式(2)计算X=0,1，…，n时的概率。今设π=0.2,n=5与25时的二项分布如图示。

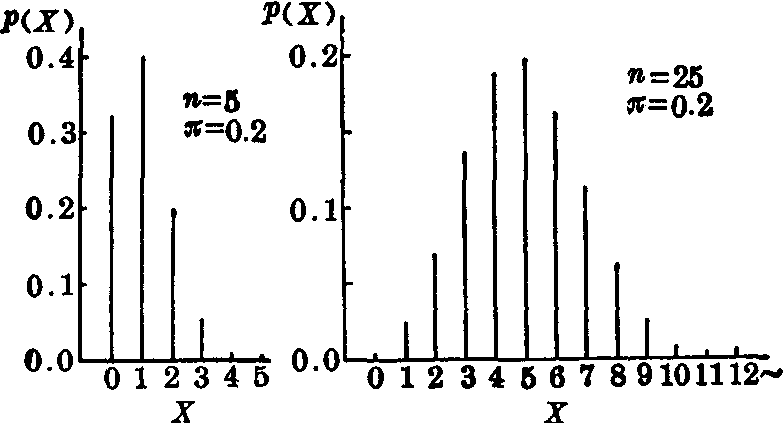
二项分布
性质 (1)均数μ、方差σ2与标准差σ分别按式(6)～(8)计算：

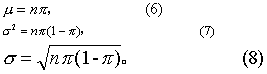
若以率表示，则分别按式(9)与(10)计算，
μp=π,(9)

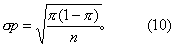
(2)正态近似式：从上图可见：当n足够大，且π不太靠近0或1时，二项分布逼近正态分布，于是式(4)中P(X)=φ(u),φ(u)为标准正态分布函数。故可按式(11)求得u值，

式中±0.5为连续性校正数，当(X-nπ)<0则+0.5，当(X-nπ)>0则-0.5；然后，查标准正态分布曲线下的面积表(见“正态分布”)，求得P(X)。
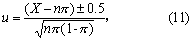
例 根据以往经验用旧药治疗某病，其治愈率x为65%，病死率为35%。今用某种新药治疗该病20人，结果有1人死亡。问该新药是否较旧药为优？设新药的治愈率π为75%，则用新药治疗该病100人，最少治愈80人的概率为多少？
假设： 新旧药疗效相同，则用新药治疗该病20人，20人全部治愈的概率，按式(2)为(0.65)²⁰，治愈19人的概率为20(0.35)(0.65)19。故最少治愈19人(即最多死1人)的概率为P=(0.65)²⁰+20(0.35)(0.65)¹⁹＝0.00213。
按检验水准α=0.05，可认为新药较旧药为优。
100名该病患者中最少治愈80名的概率，按式(5)为Q(80)，但Q(80)等于最多死亡(病死率为0.25)20人的概率P(20)。因此，先按式(11)，得

查标准正态分布曲线下面积（详表）表，当u=-1.04 时，得φ(-1.04)=0.1492，即用新药治疗100名某病患者最少治愈80人的概率为0.1492。

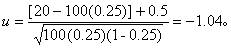
二项分布

以一次试验结果仅能产生两种事件为研究对象的分析方法。例如，一个产品经过检验，要么是合格品，要么是废品，二者必居其一。如果已知正常生产时的废品率为P( 0

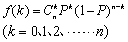
具有这种式样的概率分布叫做二项分布。式中：C_n^k是n个中取k个的组合数。

二项分布binomial distribution

描述离散随机变量的一种常用的概率分布。设在n次重复试验中，某事件出现X次的概率依次为二项展开式(X=0,1,2，……，n):
(q+p)ⁿ＝qⁿ+c¹_nq^n-1p+c²_nq^n-2p²+……+c^x_nq^n-xp^x+……+ pⁿ
式中的各相应项，其普通项常表示为：
p(x)=c^x_nq^n-xp^x＝n!/x!(n-x)!q^n-xp^x(q=1-p)上面的概率分布称为二项分布。式中p为既定事件即将发生的概率，而q为事件的曾发生的概率，指数n代表为了产生最后结果而正在运算的元素数目。二项分布的数值，决定于二项试验的次数n和每次某事件出现的概率P。二项分布的主要性质： (1)为离散分布，对固定的n和p,x取k(k=0,1,2……，n)的概率随着k的增大，先是增至最大值，然后再下降；(2)对于固定的p，随着n的增大，二项分布的图形趋于对称；(3)二项分布的期望值为np，方差为npq。它是专门描述每次试验只有发生和不发生两种可能结果的概率模型。

二项分布binomial distribution

描述离散随机变量的一种常用的概率分布。设在几次重复试验中，某事件出现X(X=0,1,2，…，n)次的概率依次为二项展开式：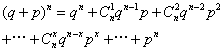
式中的各相应项，其普通项常表示为：

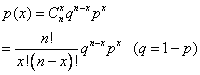
上面的概率分布称为二项分布。式中P为既定事件即将发生（成功）的概率，而q为事件不曾发生（失败）的概率。指数n代表为了产生最后结果而正在运算的元素数目。
二项分布的数值，决定于二项试验的次数n和每次某事件出现的概率p。
二项分布的主要性质：(1)二项分布为离散分布，对于固定的n和p,x取k(k=0,1,2，…n)的概率随着k的增大，先是增至最大值，然后再下降。(2)对于固定的p，随着n的增大，二项分布的图形趋于对称。(3)二项分布的期望值为np，方差为npq。二项分布是专门描述每次试验只有发生（或成功）和不发生（或失败）两种可能结果的概率模型。二项分布概率值的计算，当n很大时，则用其极限分布求其近似值较方便。

二项分布binomial distribution

亦称“贝努里分布”。离散分布的一种。仅有两种不同性质结果的概率分布。因与二项式展开式相同而得名。由瑞士数学家贝努里创始。设有n次实验，各次实验彼此独立，每次实验某事件出现的概率都是p，不出现的概率q=1-p，则对于某事件出现X次(0,1,2，…，n)的概率分布为P(x=X)=C^X_np^Xq^n-X。

二项分布

亦称“贝努里分布”。指实验中仅有两种不同性质结果的概率分布。由瑞士数学家贝努里创始。常用来描述离散型随机变量。设有n次实验，各次实验彼此独立，每次实验某事件出现的概率都是p，某事件不出现的概率q=1-p，则对于某事件出现X次(0, 1, 2, …， n)的概率分布为P(x=X)=C^X_np^Xq^n-X。