费尔马定理feierma dinsli

是微分中值定理的预备定理. 设函数f (x)在点x₀的某邻域内有定义，若函数f(x)在点x₀可导，且在点x₀处有极大值或极小值，则f′ (x₀)=0.

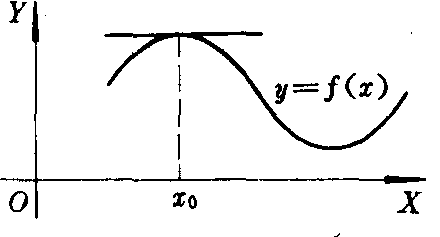
费尔马定理的几何意义如左图所示. 若函数y=f (x)在点x₀有极大值或极小值，且该曲线y=f (x)在点 (x₀,f (x₀)处有切线，则切线必平行于X轴.

---

费尔马定理feierma dingli

若P是一个质数，(a,p)=1，则a^p-1≡1(modp).这就是著名的费尔马定理.证明：因为(a,p)=1，又0,1,2，……，p-1是模p的一个完全剩余系，于是0,a,2a，…，(p-1)a也是模p的一个完全剩余系，因此，a,2a，…(p-1)a中任一个数恰与1,2，…，p-1中某一个数对模p同余，故得

a(2a)…，(p-1)a≡1·2…(p-1)(modp)

即a^p-1(p-1)!≡(p-1)!(modp).但p(p-1)!，故得a^p-1≡1(modp)，定理证毕.
有时也用稍许不同的方式来叙述费尔马定理：若p是质数，a是任一整数，则a^p≡a(modp).
利用费尔马定理可以简化求余数的计算.例如，求8⁴⁹⁵⁸除以13所得的余数.因为13是质数，(8,13)=1.故由费尔马定理可得8^12≡1(mod 13)，于是8⁴⁹⁵⁸＝(8¹²)⁴¹³·8²≡8²≡64≡-1(mod 13)，即得所求余数是12.
费尔马定理的应用很广，对数论的发展非常重要.如使用费尔马定理的逆否命题可用来判定合数：若(a,n)=1，且a^n-1≢1(modn)，则n是合数.例如，判定91是合数.令n=91，选取a=2，显然(91,2)=1.这时a^n-1＝2⁹⁰＝2⁶⁴·2¹⁶·2⁸·2².可以算出2⁸＝256≡-17(mod91),2¹⁶≡(2⁸)²≡(-17)²≡289≡16(mod91)，类似地还有2^32≡-17(mod91),2⁶4≡16(rood91). 所以

2⁹⁰ =2⁶⁴ ·2¹⁶ ·2⁸ ·2²

≡16 ·16 ·(-17)·4≡64≢1(mod91)·

得证(事实上91=7·13).用计算机处理，这种方法可判定某些十分大的数是合数. 例如费尔马数

F₅ =2²⁵ +1 =2³² +1 =4 294 967 297,

取a=3，可以验证3²³²≢1 (modF₅)，因此F5是合数·用同样的方法可以证明一些更大的费尔马数是合数·此方法的缺点是不能指出其因数是什么.
利用费尔马定理还可以证明莫森数M_p＝2^P-1的任一素因数都具有2pl+ 1的形式，其中t是一个正整数(参见 “莫森数”)