向量的分解xiangliang de fenjie

先讨论二维空间的向量分解.
定理1 若a,b不共线，则对于与a,b共面的任一非零向量r，存在唯一确定的m,n，使r=ma+nb.此处m,n不全为零.

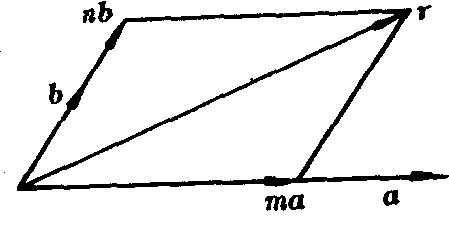
图1

这个定理表明，把不共线的向量a,b作为一个二维仿射坐标基底，则任何一个与a,b共面的向量r，都可以唯一确定地表成a,b的线性组合，或者说把r分解成了两个分别与a,b共线的向量ma和nb.见图1.
特别地，当r∥a时，r=m·a+0·b=m·a;
当r∥b时，r=0·a+n·b=n·b.
再讨论三维空间的向量分解.
定理2 若a,b,c不共面，则对于任意非零向量r，唯一存在着不全为零的m,n,l，使r=ma+nb+lc成立.
此处a,b,c构成了一个三维仿射坐标基底.

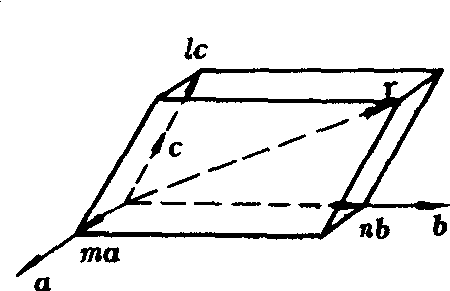
图2

❶若r不与a,b,c中任两个共面，则m,n,l全不为零.如图2所示，向量r分解成了三个分别与a,b,c共线的向量.

❷r在a,b,c中任两个向量确定的平面上，且不与基向量共线，m,n,l中有且只有一个为零.例如在a,b确定的平面上，l=0.
这是前面已讨论过的二维空间的情况.

❸r与a,b,c中某一基向量共线，则m,n,l中有且只有一个不等于零.例如与c共线，l≠0.这种极特殊的情况同样不违背定理，即r=0·a+0·b+l·c.
推论 对任意四个向量a,b,c,d，存在在不全为零的m,n,l,s，使得ma+nb+lc+sd=0.
这就是说，三维空间中任意四个向量必线性相关.