向量的向量三重积
向量的向量三重积xiangliang de xiangtiang sanchongji
两个向量叉乘,再和第三个向量叉乘,所得向量称为这三个向量的向量三重积,或称为这三个向量的二重外积.
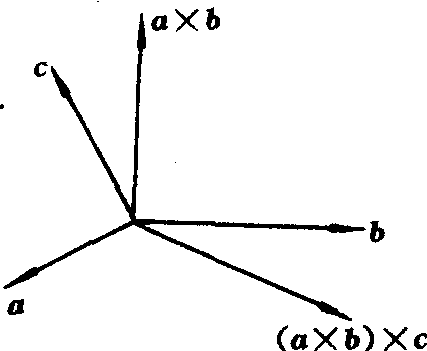
首先勾画一下向量三重积(a×b) ×c的轮廓(如图).向量a×b与a,b都垂直,且 (a×b) ×c与a×b也垂直,由 (a×b) ×c及a,b都与(a×b)垂直,得到向量(a×b) ×c与向量a,b共面,从而 (a×b) ×c必可表成a,b的线性组合.可以证明,(a×b) × c= (a ·c) b— (b ·c) a. 此式称为向量三重积展开式.
向量三重积的性质:
❶ 由向量积的负交换律可得 (a×b) ×c=-c×(a×b).
❷ 由向量积的负交换律和与数乘的结合律可得(a×b) ×c=- (b×a) ×c.
❸ 由于 (a×b) ×c是a,b的线性组合,a×(b×c)是b,c的线性组合,所以一般地有 (a×b) ×c=a× (b×c).
☚ 向量混合积的性质 多向量的乘法 ☛
- 老家衬子是什么意思
- 老家贼是什么意思
- 老家赶是什么意思
- 老家难舍,热土难离是什么意思
- 老家雀是什么意思
- 老家雀儿是什么意思
- 老家,原籍是什么意思
- 老宽是什么意思
- 老宿是什么意思
- 老寄娘是什么意思
- 老寅台是什么意思
- 老密是什么意思
- 老密处处是什么意思
- 老寇准背靴——明察暗访是什么意思
- 老寋是什么意思
- 老寡妇死了独生子——一点儿指望没有了是什么意思
- 老寡妇死了独生子——一点指望没有了是什么意思
- 老对手是什么意思
- 老寿是什么意思
- 老寿星是什么意思
- 老寿星上吊——活腻了是什么意思
- 老寿星叫门——肉头到家了是什么意思
- 老寿星吃砒霜是什么意思
- 老寿星吃砒霜——活得不耐烦了是什么意思
- 老寿星吃砒霜——活得厌了是什么意思
- 老寿星弹琵琶——老调重弹是什么意思
- 老寿星抱琵琶是什么意思
- 老寿星插草标——倚老卖老是什么意思
- 老寿星玻璃脑袋是什么意思
- 老寿星的脑袋——宝贝疙瘩是什么意思
- 老寿星骑狗——没鹿(路)了是什么意思
- 老寿星骑狗——自得其鹿是什么意思
- 老寿星骑狗——自得其鹿(乐)是什么意思
- 老寿星(彭祖)是什么意思
- 老寿木是什么意思
- 老寿柴是什么意思
- 老寿生是什么意思
- 老封君是什么意思
- 老封建是什么意思
- 老将是什么意思
- 老将偎了是什么意思
- 老将儿是什么意思
- 老将出马——一个顶俩是什么意思
- 老将出马,一个顶俩是什么意思
- 老将叱咤风云,英勇善战是什么意思
- 老将吃喽是什么意思
- 老将嚄唶是什么意思
- 老将坐了是什么意思
- 老将外了是什么意思
- 老将扛了是什么意思
- 老将撵走丧门神是什么意思
- 老将知而耄及之是什么意思
- 老将知而耄及之。是什么意思
- 老将磕咾是什么意思
- 老将至而耄及之是什么意思
- 老将舔了是什么意思
- 老将行是什么意思
- 老将行 - 唐·王维是什么意思
- 老将行 - 王维 - 少年十五二十时,步行奇得胡马骑。射杀山中白额虎,肯数邺下黄须儿。一身转战三千里,一剑曾当百万师。汉兵奋迅如霹雳,虏骑崩腾畏蒺藜。卫是什么意思
- 老尊是什么意思