向量的坐标表示xiangliang de zuobiao biaoshi

在空间直角坐标系中，分别取与X轴、Y轴、Z轴方向相同的三个单位向量i,j,k作为坐标基底，则对于任一向量a，存在唯一确定的有序实数组 (x₁,y₁,z₁)，使a = x₁i+y₁i+ z₁k，如图所示. (x₁,y₁,z₁)叫作a在取定的坐标基底下的坐标，x₁,y₁,z₁分别叫a在X轴、Y轴、Z轴上的坐标分量.

若向量a是点A的位置向量，显然此时点A的坐标就是向量a的坐 标，即A (x₁,y₁,z₁ ),a= (x₁,y₁,z₁).
特别地，i=(1,0,0),j= (0,1,0),k=(0,0,1),0=(0,0,0).
由于a恰为以x₁i,y₁j,z₁k为棱的长方体的对角线，所以a的模长为

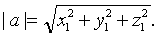
设a= (x₁,y₁,z₁ ),b=(x₂,y₂,z₂),c= (x₃,y₃,z₃).
❶ 两向量和的坐标等于两向量相应坐标的和. a+b= (x₁+x₂,y₁+y₂,z₁+z₂).

❷ 两向量差的坐标等于两向量相应坐标的差. a—b= (x₁—x₂,y₁—y₂,z₁—z₂).
由于起点为M(m₁,m₂,m₃)，终点为N (n₁,n₂,n₃)的向量N与N-M相等，从而

这与空间解析几何中两点间距离公式是完全一致的.
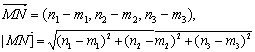
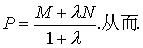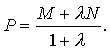若M= (m₁,m₂,m₃),N=(n₁,n₂,n₃)，定比分点P的位置向量P= (P₁,P₂,P₃)，且则从而 .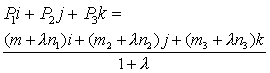

由向量线性表出的唯一性，得到

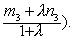
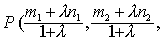
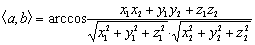定比分点P的坐标可表示为这与平面几何中的定比分点公式是一致的.

❸ 数乘向量，所得向量的坐标等于用这个数乘原来向量的相应坐标. ka= (kx1,ky1,kz1).

❹ 两向量的数量积等于这两个向量相应坐标的乘积的和a ·b=x₁x₂+y₁y₂+z1z₂.
向量a与b垂直的充要条件是x₁x₂+y₁y₂+z₁z₂ =0.
两非零向量a与b的夹角可用坐标表示为

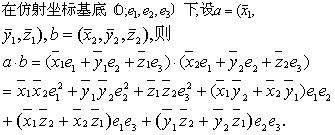
用向量a的坐标表示其方向余弦

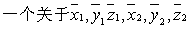
在仿射坐标基底 [O; e₁, e₂, e₃]下，设a= (₁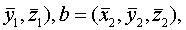

则

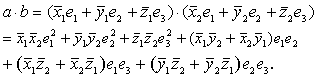
这表明，a · b是a和b的坐标的齐二次式，任意一个关于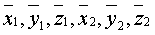的齐二次式都可以看作是两个向量在某一仿射坐标基底下的内积. 并且，当仿射坐标基底取得最好 （正交） 时，相应的齐二次式最简单.

❺ 两向量的向量积的坐标表示

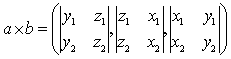
注意到i×i=j×j=k×k=0,i×j=k,j×k=i,k×i=j，很容易得此结果.
向量a与b共线的充要条件是

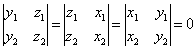
或者

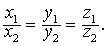
根据三阶行列式的性质，a×b还可表示为

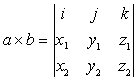
用向量积的坐标表示两个非零向量的夹角

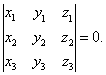
❻ 三向量的混合积的坐标表示为

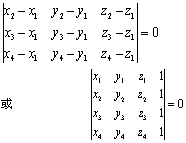
当a,b,c成右手系时，行列式的值为正.
当a,b,c成左手系时，行列式的值为负.
三向量共面的充要条件是

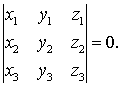
❼ 空间四点A (x1,y1,z1),B (x₂,y₂,z₂),C(x₃,y₃,z₃),D (x₄,y₄,z₄)共面的充要条件是

或

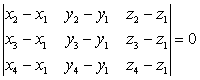
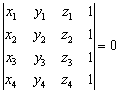
这是空间三向量B,C和D的坐标转而用四点的位置向量的坐标表示的结果.