向量混合积的性质siangliang hunheji de xing zhi

❶ 由数量积的交换律可得a×b ·c=c ·a×b.

❷ 由向量积的负交换律可得a×b ·c=-b×a · c.

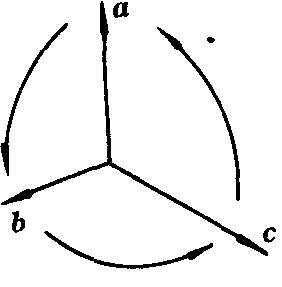
❸ 由于混合积 (a,b,c)的绝对值是以a,b,c为棱的平行六面体的体积 (参见 “向量混合积的几何意义”)，且轮回置换后手系不变 （如图），所以a×b ·c=a ·b×c ·a.又由第1条性质b×c ·a=a · b×c，所以a×b ·c=a·b×c. 即点乘、叉乘可以互换.从而得到a,b,c的十二个混合积之间的关系是a×b· c=a · b×c=b×c · a=b · c×a=c×a · b=c · a×b=-b×a ·c=-b ·a×c=-a×c · b=-n ·c×b=-c×b · a=-c · b× a.

❹ (ka,a,b) =0. 这是因为 (ka,a,b) =ka×a ·b=0 ·b=0.从几何意义上看.在平行六面体中，其顶点的三条棱不能有两条棱共线.

❺ (a,b,c+d) = (a,b,c)+ (a,b,d). 这是因为，(a,b,c + d) =a×b · (c+d) =a×b ·c+a×b · d.
综合
❹,
❺可得 (a,b,ma+nb)=0. 其几何意义是三个共面向量无法构成平行六面体.

❻ (ka,b,c) =k (a,b,c). 根据数量积和向量积的与数乘的结合律有 (ka,b,c) = (ka) ×b ·c= [k (a×b)] ·c=k (a×b ·c) =k (a,b,c).