理查兹方程Richards equation
描述生物种群消长的数学模型。范·伯塔兰菲(L.Von Ber-talanffy,1938,1957)最早提出动物体重的变化与合成和分解代谢速率成比例,在种群y<1/e时用这些过程的速率描述。理查兹(F.J.Richards,1959)将范·伯塔兰菲模型推衍为生长速度或瞬时速率即dy/dt随t而变的曲线,提出以下形式的可塑性生长模型:
dy/dt=rRy(1-ym-1)/(m-1)
式中,rR为速率参数; m为斜率参数,其值可以从0到无限大。当m=0时,模型可转化为指数模型,当m=2时,则转化为逻辑斯蒂模型(见逻辑斯蒂模型),而m接近1时可转化变为冈伯茨模型(见冈伯茨方程)。因此,这是一个可塑性很强的模型(见图)。该模型的积分形式为: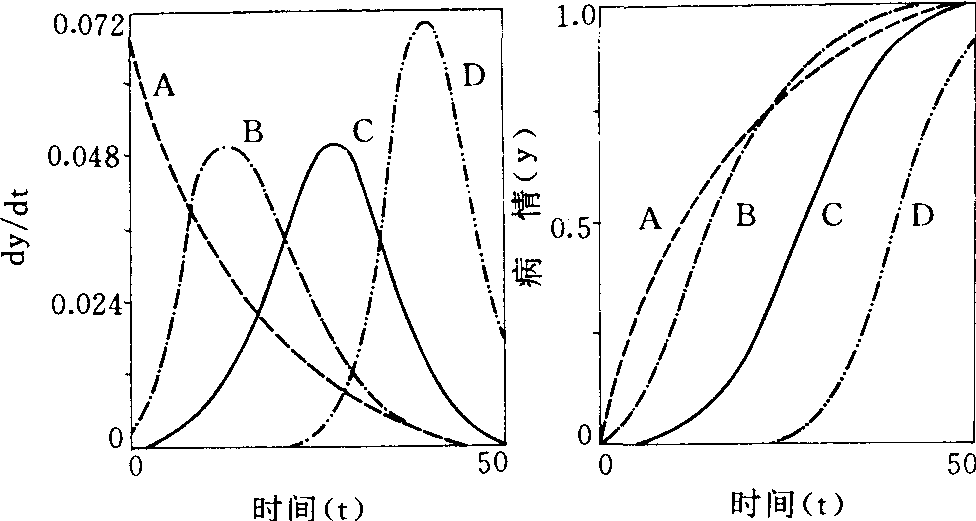
理查兹模型曲线
A:m=0.0; B:m=1.0; C:m=2.0; D:m=2.7
y=[1-B exp (-rRt)]1/(1-m) (m<1)
y=[1+Bexp(-rRt)]1/(1-n) (m>1)
1n{1/[1-y(1-m)]}=-1n(B) +rRt (m<1)
1n{1/[y(1-m)-1]}=-1n(B)+rRt (m>1)
- 沈宗瀚是什么意思
- 沈宗灵是什么意思
- 沈宗琳是什么意思
- 沈宗畸是什么意思
- 沈宗确是什么意思
- 沈宗约是什么意思
- 沈宗翰是什么意思
- 沈宗騫是什么意思
- 沈宗骞是什么意思
- 沈宗骞竹林听泉图轴是什么意思
- 沈定是什么意思
- 沈定一是什么意思
- 沈定钧是什么意思
- 沈宛是什么意思
- 沈宜修是什么意思
- 沈宜甲是什么意思
- 沈宝善是什么意思
- 沈宝基是什么意思
- 沈宝昌是什么意思
- 沈宝爱是什么意思
- 沈宝珠是什么意思
- 沈宝谦是什么意思
- 沈宠是什么意思
- 沈宠绥是什么意思
- 沈客卿是什么意思
- 沈宪楙是什么意思
- 沈宪英是什么意思
- 沈家台遗址是什么意思
- 沈家同是什么意思
- 沈家园是什么意思
- 沈家围子遗址是什么意思
- 沈家大屋是什么意思
- 沈家大屋会议是什么意思
- 沈家妮是什么意思
- 沈家彝是什么意思
- 沈家本是什么意思
- 沈家村石狮与辟邪是什么意思
- 沈家杰是什么意思
- 沈家桢是什么意思
- 沈家沟是什么意思
- 沈家社区是什么意思
- 沈家祥是什么意思
- 沈家立是什么意思
- 沈家脾是什么意思
- 沈家銘是什么意思
- 沈家铭是什么意思
- 沈家门是什么意思
- 沈家骐是什么意思
- 沈家骢是什么意思
- 沈宸凤是什么意思
- 沈寂是什么意思
- 沈寄簃先生遗书是什么意思
- 沈寄簃先生遗书甲编是什么意思
- 沈寄踪是什么意思
- 沈寅是什么意思
- 沈寅初是什么意思
- 沈寅驭是什么意思
- 沈富是什么意思
- 沈寐叟是什么意思
- 沈寒柯是什么意思