最小二乘法zuixiao erchengfa

19世纪初，著名数学家高斯和P. S. 拉普拉斯由于研究误差分析而引进了最小二乘法，这个方法经过A. A.马尔可夫等许多学者的发展，成为统计分析上一个极为重要的方法。
最小二乘法原理如下：
设y是变量x₁ ,x₂ ，…，x_n的函数，含有k个参数a₁,a₂，“ …，a_k。即

y =f(a₁,a₂，…，a_k;x₁,x₂，…，x_m)。

今对y和x₁,x₂，…，xm作n次观测得(x_1i,x _2i，…，x_mi;y i) (i=1, 2, …， n)，于是y的理论值＝f (a₁ ,a₂ ，…，a_k; x_1i,x _2i，…，x_mi)与观察值yi的绝对误差为|y_i-_i| (i=1, 2，…， n)，式中有绝对值记号，不便于进一步分析讨论，由于任何实数的平方都是正数或零，因此，可以要求上面n个误差在平方和最小的意义下，使得函数y=f (a₁,a₂，…，a_k ; x_i1 ,x_i2，…，x_im)与观测值y₁,y₂，…，y _n最佳拟合，也就是参数a₁ ,a₂，…，a_k应使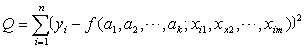

　=最小值
由微分学的求极值方法可知a₁,a₂ ，…，a_k应满足下列方程组

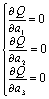
这种根据偏差的平方和为最小的条件来选择参数a ₁,a ₂ ，…，a _k的方法叫做最小二乘法。

最小二乘法

一种常用的数学方法。在实验中获得了自变量与因变量的若干个数对(x₁,y₁),(x₂,y₂)，…，(x_n,y_n)，要找出一个已知类型的函数y=f(x)(如线性函数y=ax+b等)，使得偏差平分和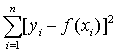最小。 常用于工程技术和科学研究的数据处理。

最小二乘法least square method

是由样本观察值估计总体参数的一种方法。它要求各观察值和估计量的差的平方和为最小。

最小二乘法

考虑一个简单的例子。对x的一系列选定值x₁,x₂，…，x_n，测出了y的相应值y₁,y₂，…，y_n, 且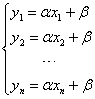

现要求出α和β的最佳值满足以上线性方程组。设ηi=y_i—(αxi+β)，利用最小而求出α和β使xi和y_i最大限度地满足y=αx+β，这个近似表达式叫经验公式，这种根据偏差ηi的平方和为最小的条件来选择常数α和β的方法，叫最小二乘法。对上例，利用函数的极值条件有：

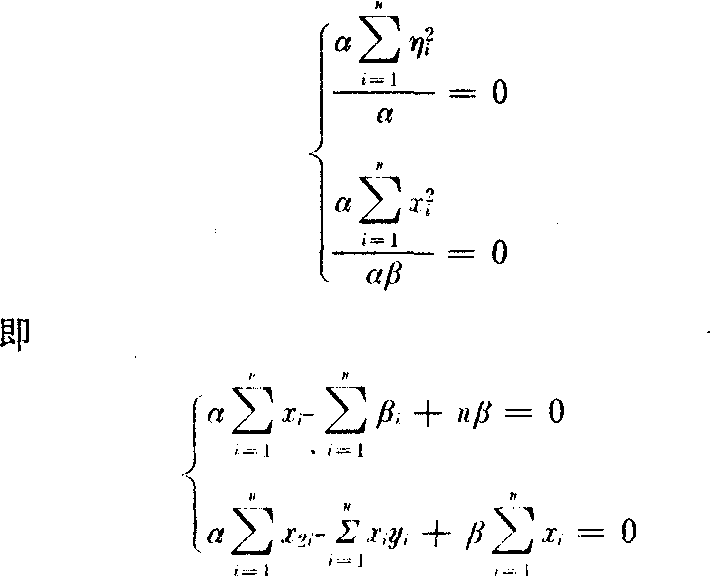
由此求出α和β。经验表明，在一般情况下，这样确定的经验公式可以很好地拟合给定的数据。最小二乘法是由勒让德提出的，在实践中应用广泛。

最小二乘法

亦称“最小平方法”。一种常用的数学方法。在处理实验数据计算回归方程系数，确定回归直线时，它使所确定的回归直线与所有观测值之差的平方和为最小。设有随机变量X和Y的n对观测值(x1,y1)，……，(xn,yn)，但不知道X和Y之间的精确数学关系式。为了求得它们之间的近似关系式，首先假定此关系式是一个系数未定的多项式(例如线性函数f(x)=ax+b)，然后依据“使观测值与由回归方程计算出来的值的差的平方和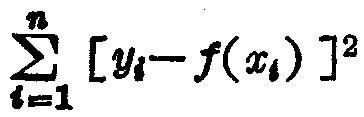为最小”的准则计算出各系数的值，借此获得回归直线的数学关系式。一般地，利用最小二 乘法，能尽量消除偶然误差的影响，从而由一组观测数据求出最可靠、最可能出现的结果来。

最小二乘法Least-square Method

亦称“最小平方法”。一种常用的回归分析方法。是进行回归分析的基础。通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

最小二乘法

在经济计量模型中一种常用的参数估计方法。这种方法可使最终由模型计算出来的因变量的估计值与其实际值之差的平方和最小。参见“经济计量模型”。

最小二乘法

亦称 “最小平方法”。使对因变量的估计值与实际观测值之差的平方达到最小。目前常见的回归分析方法之一，是进行回归分析的基础。又被称作“ordinary least quare” (可译为 “普通最小二乘法” 或 “普通最小平方法”)。这一方法最早由勒让德提出，后经G. F. Guass和P. S. Laplace引入统计学研究之中。下面用一个线性回归模型来具体说明这一方法。对于回归模型：

Y= Zβ+ε

有　ε = Y-Ŷ

式中，Y是被解释变量向量； Z是解释变量向量； u是白噪声向量； 其均值为零，方差为σ2;β是待估参数。最小二乘法要求待估的回归方程使得的平方和达到最小，即：

＝ (Y-Zβ)′(Y-Zβ) =最小

因为Y和Z是已知的，的大小完全取决于β的大小，而β是由估计方法确定的参数。因此，根据微积分中求极值的原理，当β的一阶导数等于零时，才能达到最小值，因而有：

/α(Y-Zβ)′ (Y-Zβ)=0

整理后有常规方程： (Z′Z)β= Z′Y
如果 (Z′Z)-1存在，以上常规方程有解：

β= (Z′Z)-¹Z′Y

β就是回归模型Y= Zβ+ε的普通最小二乘估计值， 它使′ε达到最小。
由于现实生活中往往出现违背线性回归模型的基本假设，如异方差性、多重共线性、残差自相关等等，以致矩阵 (Z′Z)近于退化，很难用普通最小二乘法进行模型参数估计。为此出现了基于它的一些更为一般和适用的方法，如广义最小二乘法、加权最小二乘法、间接最小二乘法、工具变量法、约束最小二乘法等等。

最小二乘法least square

亦称“最小平方法”。使对因变量的估计值与实际观测值之差的平方达到最小。目前常见的回归分析方法之一，是进行回归分析的基础。又被称作“ordinary least quare”(可译为“普通最小二乘法”或“普通最小平方法”)。这一方法最早由勒让德提出，后经G.F.Guass和P.S.Laplace引入统计学研究之中。下面用一个线性回归模型来具体说明这一方法。
对于回归模型：

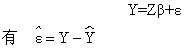
式中，Y是被解释变量向量；Z是解释变量向量；u是白噪声向量；其均值为零，方差为σ²;β是待估参数。最小二乘法要求待估的回归方程使得的平方和达到最小，即：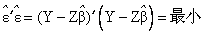

因为Y和Z是已知的，的大小完全取决于的大小，而是由估计方法确定的参数。因此，根据微积分中求极值的原理，当的一阶导数等于零时，才能达到最小值，因而有：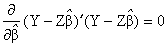

整理后有常规方程：(Z'Z)＝Z'Y
如果(Z′Z)^-1存在，以上常规方程有解：

＝(Z′Z)^-1Z′Y

就是回归模型Y=Zβ+ε的普通最小二乘估计值，它使达到最小。
由于现实生活中往往出现违背线性回归模型的基本假设，如异方差性、多重共线性、残差自相关等等，以致矩阵(Z′Z)近于退化，很难用普通最小二乘法进行模型参数估计。为此出现了基于它的一些更为一般和适用的方法，如广义最小二乘法、加权最小二乘法、间接最小二乘法、工具变量法、约束最小二乘法等等。

最小二乘法

最小二乘法(A. M. Legendre,1752～1833)亦称最小平方法，是一种误差控制的基本方法，常用于回归分析和方差分析等方面。本法原理可用最简单的直线回归来说明。
将每一对数据(X_i,Y_i)在方格坐标纸上描点。如果这些点子呈直线趋势，则可用目测法穿过这些点子拟合一直线，如图所示。但用目测法拟合的直线主观性大，一般

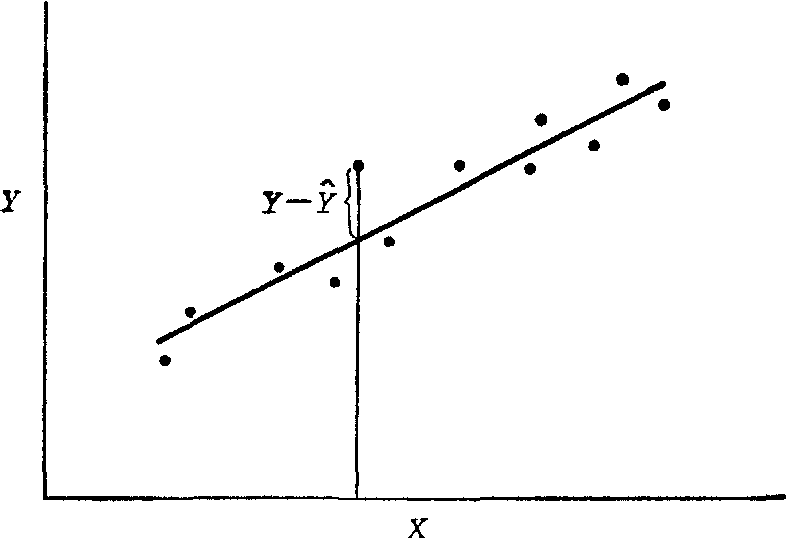
Y对X的回归直线

因人而异，如用最小二乘法拟合直线，则将获得唯一的“最优”结果。最小二乘法的原理是使拟合的直线方程

Ŷ=a+bX (1)

中的Y与相应的观察值Y之差的平方和，即∑(Y-Ŷ)²为最小。从上图来说，也就是各观察点至直线的纵向距离的平方和为最小。
根据上述原则，利用数学分析中求极值的方法可求得：

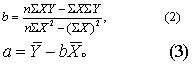
将求得的a与b值代入式(1)，即得所需的直线方程。

最小二乘法

又称最小平方法。其基本原理是使实际值与趋势值的离差的平方和为最小，以此拟合优良的趋势模型，从而测定长期趋势。

最小二乘法

也称“最小平方法”。一种确定空间平而上几个有线性关系趋势的点(x₁,y₁),(x₂,y₂)，……(x, y), 求一估计直线（或曲线）与实际观测值之差的平方和为最小的方法。这是研究经济现象发展趋势的常用方法之一。估计直线所描绘发展趋势基本为直线型，估计曲线所描绘的趋势往往呈曲线（常用抛物线型或指数曲线型）。

最小二乘法least-squares principle

分为“普通最小二乘法”(Ordinary Least Squares简称OLS)和“广义最小二乘法”(Generalized Least Squares简称GLS)。
普通最小二乘法是适用于[经典线性回归模型]的估计参数的方法。对于经典线性回归方程：

Y=Xβ+u

根据X和Y的样本数据来估计参数β，设估计值为，则：

Y=X+e

Y的估计值＝X，所以e=Y-X＝Y-是Y的估计误差。最小二乘法的基本思想是：如果令误差平方和e′e最小，那么估计值Y是最接近原值Y的(注意Y和e均为向量，e′表示e的转置)。由微分学的求极值方法

可推导出：

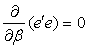
β=(X′X)^-1X′Y

据[高斯—马尔可夫定理]，对于经典线性回归模型使用普通最小二乘法，所得的参数估计式(即此处的β)是最优线性无偏估计式。
广义最小二乘法适用于违反经典假定的线性回归模型，设模型为：

Y=Xβ+u

假定E(u)=0,E(uu′)=σ²Ω，其中σ²为常数，Ω为n阶对称正定矩阵，包含了异方差和（或）自相关的信息。
经过模型变换和推导，得到β的广义最小二乘估计式为：

β=(X′Ω^-1X)^-1X′Ω^-1Y

据[高斯—马尔可夫定理]，对于违反经典假定的线性回归模型，广义最小二乘估计式(即此处的)是最优线性无偏估计式。

最小二乘法

亦称“最小平方法”。对一列统计观察数据，配合一条理论曲线，使所有观察值与理论曲线上对应的估计值的偏差的平方和为最小的方法。设有变量x和y的n对观察值(x1,y1)、(x2,y2)、…… (xn, yn) ，再求得理论曲线ŷ=f(x), 使其偏差平方和∑[yi-f(xi)]2为最小。例如，有理论线ŷ_i＝a+bx_i, 欲使∑[y_i-(a+bx_i)]²＝G为最小，必须使

解得：

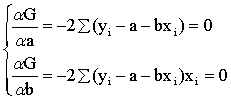
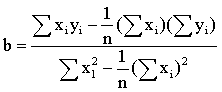
a=-b
将数据资料代入方程求得a和b的估计值，从而就得到了用最小二乘法求出的理论线ŷ_i＝a+bx_i。

最小二乘法square method

根据变量的一系列观测数据，按误差平方和最小的原则来建立变量之间的最优数学关系的方法，又称“最小平方法”。它是统计中常用的参数估计方法之一。指在确定一个己知类型函数的曲线时，使所有观察值与该曲线上的对应点之偏差的平方和为最小。设随机变量x和y的几对观察值为(x1y1),(x₂y₂)…(_xn_yn)，在求得己知类型的函数y=f(x), 使其偏差平方和[y_i-f(x_i)]²为最小。这种求f(x)的方法，就称作最小二乘法。最小二乘法在回归分析、主成分分析、因素分析等多元分析法中均有应用。