刘徽原理
041 刘徽原理
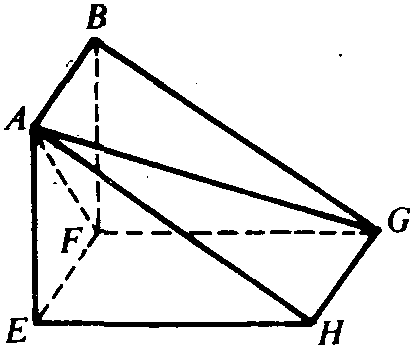
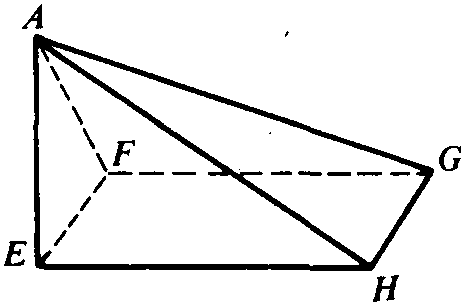
刘徽在《九章算术注》的阳马术注文中给出的关于多面体体积的重要原理。原文为：“阳马居二、鳖臑居一，不易之率也。”其意为： 将一个堑堵(长方体被其对角面分割后得到的楔形体)斜向分解为一个阳马(直角四棱锥)和一个鳖臑(各面均为直角三角形的四面体)(见图)，则阳马与鳖臑的体积之比恒为2:1。刘徽用极限方法证明了上述原理。由刘徽原理易得阳马、鳖臑体积公式：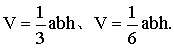
(a、b、h分别为长方体的长、宽、高)，进而得到四面体体积公式：V=1/3S底h。刘徽还指出：圆锥、圆亭(圆台)各与其外切方锥(正四棱锥)、方亭(正四棱台)之体积比为π:4，并由此证明了圆锥、圆亭体积公式。刘徽的这些思想为后世祖暅原理的提出和球体积公式的证明奠定了基础。刘徽原理是中国古代几何学中体积理论的基础。
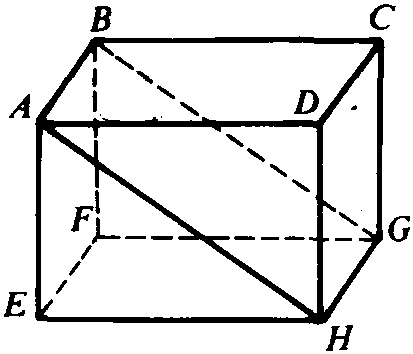
长方体
堑堵
阳马
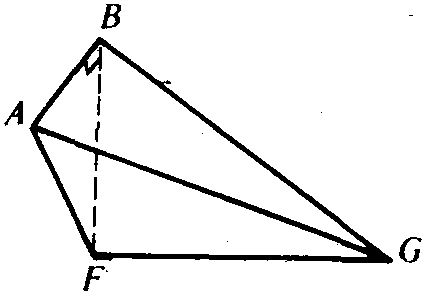
鳖臑
☚ 出入相补原理 割圆术 ☛
- 首航封是什么意思
- 首舵是什么意思
- 首荐是什么意思
- 首虏是什么意思
- 首虐是什么意思
- 首行缩排（缩格）是什么意思
- 首裨山是什么意思
- 首要是什么意思
- 首要公众是什么意思
- 首要分子是什么意思
- 首要性格是什么意思
- 首要条款是什么意思
- 首要案例是什么意思
- 首要特质是什么意思
- 首要的事是什么意思
- 首要的事务是什么意思
- 首要的方法是什么意思
- 首要职务是什么意思
- 首要问题是什么意思
- 首言是什么意思
- 首计是什么意思
- 首议是什么意思
- 首访是什么意思
- 首评是什么意思
- 首诊是什么意思
- 首诊责任制是什么意思
- 首译是什么意思
- 首调唱名法是什么意思
- 首调读谱法是什么意思
- 首谋是什么意思
- 首谋倡议是什么意思
- 首象印是什么意思
- 首贼是什么意思
- 首赞五十易，又删三百诗。是什么意思
- 首超是什么意思
- 首足是什么意思
- 首足异处是什么意思
- 首路是什么意思
- 首身是什么意思
- 首身分离是什么意思
- 首身分裂是什么意思
- 首身离是什么意思
- 首身離是什么意思
- 首车是什么意思
- 首车风雨桥是什么意思
- 首轮放映是什么意思
- 首轮放映的电影是什么意思
- 首轮电影院是什么意思
- 首辅是什么意思
- 首过是什么意思
- 首过效应是什么意思
- 首逆是什么意思
- 首选是什么意思
- 首途是什么意思
- 首途运输是什么意思
- 首造是什么意思
- 首邱是什么意思
- 首 部是什么意思
- 首部是什么意思
- 首都是什么意思