比较两个风险资产哪一个较优的一种方法。
在一个有n种状态的市场上,状态i发生的概率为pi,i=1,2,…,n,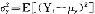 pi=1,pi≥0。一个风险资产
pi=1,pi≥0。一个风险资产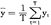 用一个状态-财富向量
用一个状态-财富向量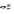 =(c1,c2,…,cn)表示,其中ci是状态i发生时,风险资产
=(c1,c2,…,cn)表示,其中ci是状态i发生时,风险资产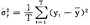 的财富。设还存在另一个风险资产
的财富。设还存在另一个风险资产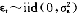 =(d1,d2,…,dn)。一个投资者的偏好由效用函数v(·)表示,如果
=(d1,d2,…,dn)。一个投资者的偏好由效用函数v(·)表示,如果
E[v(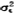 )]>E[v(d)] (1)
)]>E[v(d)] (1)
则认为资产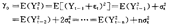 比
比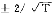 好。
好。
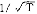 和
和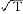 的积累概率分布函数分别为F(e)=Pr{
的积累概率分布函数分别为F(e)=Pr{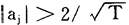 ≤e}和G(e)=Pr{
≤e}和G(e)=Pr{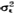 ≤e},它们的概率密度函数分别为f(e)=F′(e)和g(e)=G′(e)。则(1)式等价于
≤e},它们的概率密度函数分别为f(e)=F′(e)和g(e)=G′(e)。则(1)式等价于
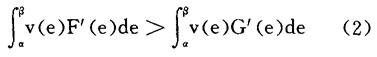
其中α和β为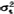 和
和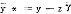 取值的下、上限、易于看出,如果下列条件成立:
取值的下、上限、易于看出,如果下列条件成立:
F(e)≤G(e),对所有e∈[α,β] (3)
且 F(ej)<G(ej),对某一个ej
则当v(·)是增函数时,(1)式必成立,即投资者认为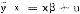 优于
优于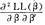 。
。
当条件(3)成立时,就称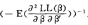 一阶随机占优于
一阶随机占优于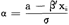 。条件(3)从图形看,相当于对任何一个e,F(e)的图形总位于G(e)的下方。
。条件(3)从图形看,相当于对任何一个e,F(e)的图形总位于G(e)的下方。
当曲线F(e)和G(e)有交点且相互穿过时,条件(3)不成立。
但若下列条件成立:
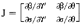 F(r)dr≤
F(r)dr≤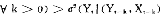 G(r)dr,对所有e (4)
G(r)dr,对所有e (4)
且 F(ei)≠G(ei),对某一个ei
则当v′>0及v″<0时,(1)式必成立。当条件(4)成立时,称#二阶随机占优于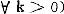 。
。
- 对外贸易是什么意思
- 对外贸易体制改革是什么意思
- 对外贸易的发展战略是什么意思
- 对外贸易的经济效益是什么意思
- 对外贸易行纪合同是什么意思
- 对女性病人体检有什么要求是什么意思
- 对妊娠有危害性的药物是什么意思
- 对存在风险的金属的分析是什么意思
- 对宗教政策的研究是什么意思
- 对定型包装食品的商品标志有什么要求?是什么意思
- 对-(对-甲苯基磺酰胺基)二苯胺或N-(对-甲苯磺酰胺基)-N′-苯基对苯二胺是什么意思
- 对少年犯的刑罚措施是什么意思
- 对工会企事业的从业人员如何管理?是什么意思
- 对工会兴办企事业的审查要求和方法有哪些?是什么意思
- 对工会兴办的企事业审查的目的是什么?是什么意思
- 对工会领导班子知识和专业结构有哪些要求?是什么意思
- 对工商行政管理局做出的罚款决定,商标注册人和未注册商标使用人不服怎么办?是什么意思
- 对工艺方案的基本要求是什么意思
- 对帐是什么意思
- 对帐的具体内容有哪些?是什么意思
- 对常熟市土地管理局关于村民跨村、乡(镇)占用集体非耕地建房问题的请示的答复是什么意思
- 对干制食品的基本要求是什么意思
- 对库存货物的套期保值或融资是什么意思
- 对-异丙氧基二苯胺是什么意思
- 对异氰酸酯有高活性的聚醚多元醇是什么意思
- 对异议裁定的商标能否再以相同的事实理由申请争议裁定?是什么意思
- 对弧焊电源的基本要求是什么意思
- 对待来大陆探亲旅游的台湾宗教人员的原则是什么意思
- 对性病病人体检时要注意哪些事项是什么意思
- 对成吉思汗的研究是什么意思
- 对成革质量影响较大的缺陷是什么意思
- 对我国古代球状石墨铸铁的研究是什么意思
- 对或有风险进行分析的详细步骤是什么意思
- 对所使用的合约条款的概述是什么意思
- 对手工电弧焊电源的要求是什么意思
- 对执法过错责任人的处理是什么意思
- 对执行环境保护法有些什么具体措施?是什么意思
- 对接接头单面焊是什么意思
- 对接接头双面焊是什么意思
- 对接焊缝的强度计算是什么意思
- 对数人同时犯罪的检控是什么意思
- 对新建食品生产经营企业和利用新资源生产的食品新品种的食品卫生管理有哪些要求?是什么意思
- 对无能力状况进行复查的诉讼程序是什么意思
- 对有争论的特殊应用问题的材料选择是什么意思
- 对有关问题进行咨询是什么意思
- 对期权的估价是什么意思
- 对期权的基本运用是什么意思
- 对未分配利润如何理解?是什么意思
- 对未成年人不良行为的预防是什么意思
- 对未成年人不良行为的预防是什么意思
- 对未成年人严重不良行为的矫治是什么意思
- 对未成年人严重不良行为的矫治是什么意思
- 对未成年人重新犯罪的预防是什么意思
- 对未成年人重新犯罪的预防是什么意思
- 对未按规定保管增值税专用发票的处罚是什么意思
- 对未按规定开具增值税专用发票的处罚是什么意思
- 对某些产品进口的紧急措施是什么意思
- 对标准化系统的一般分析是什么意思
- 对校办企业征收增值税的政策是什么意思
- 对毒性药品如何管理?是什么意思