调整成本tiáo zhěng chéng běnрегулрование себестóимости (издéржек, затрт)

调整成本Adjustment cost

指某个决策变量改变时，经济个体所发生的成本。在经济个体的最优化模型中引入调整成本，是为了导出决策变量的最优变化率，并为调整选择变量以改变外生变量而发生的时滞建立的一个理论说明。调整成本分为：内部和外部调整成本。内部是指厂商将资本和劳动等生产要素从生产领域转向新投资活动所放弃的产量。其中由于进行研究、开发和规划管理以及安装新设备时都需要使用企业的一部分资源，从而造成产量的下降，这就产生了内部调整成本。投资规模越大，内部调整成本就越高。外部调整成本是指如果厂商在相应的资本品市场上处于买方垄断地位，由于厂商对资本品需求的上升所引起的资本品价格的上涨。厂商的投资规模越大，单位时间内购买的资本品越多，由于价格上涨所需支付的额外费用越高，外部调整成本越大。调整成本的引入对投资理论具有十分重要的意义。新古典静态厂商理论的主要问题是，对资本的需求只能被视为一种存量，而不是对投资的不断需求，因此使用该模型无法正确地预测实际利率的上升（下降）会导致个别厂商对厂房与设备的投资出现下降（上升）。只有引入了调整成本以后，才能合理地解释个别厂商对投资的有限需求，并在理论上说明个别企业的投资率与实际利率之间的相互联系。

调整成本adjustment cost

调整成本是指决策变量发生变动时经济个体所发生的成本。调整成本根据其产生的原因不同，可以划分为由厂商的内部活动引起的内部调整的成本和由厂商外部的市场力量引起的外部调整的成本。
内部调整的成本是指厂商将资源由生产活动转向投资活动时所必须发生的一部分成本。它主要包括计划成本和安装费用。在制定投资计划时，研究、开发和管理活动中要使用资源。同样地，新资本的装备也要在“固定”新资本品、重组生产线和培训工人及使用新设备等方面耗用资源。这些活动上所损失的产出构成调整的成本。而且，投资率越大，有关的成本也就越大。
当厂商在资本品市场上是一个独家垄断者时，就会产生外部调整的成本。在资本为厂商高度专有时，个别厂商对资本的需求，可能占有该类资本市场的需求的很大一部分，这时就很可能产生买主垄断的势力。在此情况下，厂商面临一个上升的资本品供给价格。单位时间购买的资本品越多，即投资率越高，它必须以较高价格的形式支付一笔额外费用。
调整成本之所以出现在经济个体的最优化模型中，是为了给区别于最优水平的决策变量的最优变化率的导出提供一个基础，并为调整选择变量的最优变化率而发生的时滞提供一个理论说明。设一个在时间t时面对价格P(t)的厂商，选择时间t时的投资存量K(t)及L(t)，并且最优资本变化率(t)以最大化其未来利润贴现值之和，用公式表示即求下式最大值：

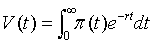
其中π(t)=P(t)Q(t)-W(t)L(t)-G(t)

(t)-C[(t)]

而Q(t)=F[K(t),L(t)]
式中，V为企业利润的贴现值，π为净收益，Q为产量，L为劳动服务，为投资，K为资本存量，P为价格，W为工资，G为资本品价格，r为名义利率，C(K)就是所谓的调整成本，小圆点表示对时间求导。
一家厂商在决定今天增加投资是否可取时不仅基于要达到更高的生产水平而增加的成本，也基于调整成本要受到多大影响。通过引入调整成本，对上述最优化问题求最大值，就可求出一个最优的投资函数(t)，即资本存量的变化率。