正态分布

又称“高斯分布”、“常态分布”。是一种连续型随机变量的分布。如果随机变量X的概率密度函数为：

则称X服从参数为μ与σ的正态分布，记为X~N(μ,σ²)。在概率论与数理统计的各种分布中居于首要地位。常被应用于测验分数统计中。

正态分布normal distribution

连续性变数的一种最主要的理论分布。它是二项分布的极限形式。如果随机变量ξ的概率密度为：

则称ξ服从正态分布N(μ,σ²)。正态分布曲线以算术平均数μ为原点，方差为σ²，向左右两侧作对称分布，并以x轴为渐近线。其多数次数集中在μ附近；离平均数愈远，分布次数愈少，呈中间高两头低的钟形曲线。算术平均数、中数和众数在|x=μ|=1σ处有拐点。它以参数μ和σ的不同而表现为一系列曲线，与x轴之间的总面积等于1。曲线上任意区间的面积等于x落于这个区间内的概率。μ=0,σ²＝1的正态分布，即N(0,1)，称为标准正态分布。

正态分布zhengtai fenbu

指一种两头小、中间大而隆起、两边对称并呈“钟形”的特定概率分布，其数学表达式为

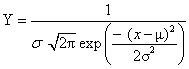
式中 Y——频率（相对次数）
μ——总体平均数
σ——总体标准差
x——随机变量
π——常数(约为3.14159)
exp——常数(约为2.71828)
从式中可见：正态分布曲线是由μ和σ所决定的；当μ与σ不同时，就有不同的正态分布曲线。若用z=x-μ/σ代入上式，即平均数为0、标准差为1时，则变为

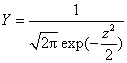
这就是标准正态分布。也就是我们通常所说的正态分布，其Y值可从正态曲线的纵线表中查到。
正态分布曲线有下列性质：
❶曲线以z=0为中心，两边也对称；
❷曲线在z=0处有最大的频率(Y=＝0.3989);
❸曲线在z=±1处有两个拐点；
❹曲线下面的面积为1;
❺曲线两端向基线无限延长、接近基线，但永远不与基线相交。
正态分布下的面积与μ、σ有下列关系：以平均数为中心向两边各取1个标准差(即μ±σ)，其范围约占总面积的68.26%；若向两边各取2个标准差(即μ±2σ)，则其范围约占总面积的95.45%；若向两边各取3个标准差(即μ±3σ)，则其范围约占总面积的99.73%。

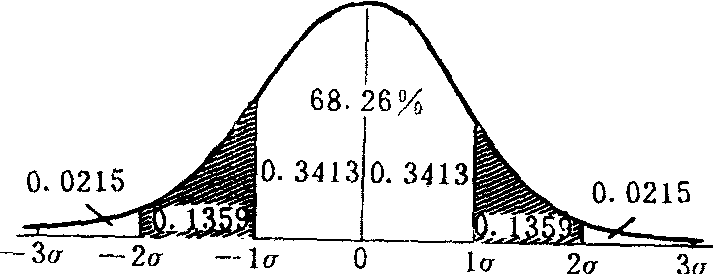
正态曲线下不同σ单位之间占总面积的比例

正态分布在数理统计中是最重要的一种分布。由于教育与心理上许多现象(如学习成绩、智力水平、身高体重、感觉阈限等)的数据分布服从或近似服从正态分布，因而它在教育研究中有极重要的地位和广泛的应用。

---

正态分布zhengtai fenbu

设连续型随机变量X的概率密度为

其中μ,σ> 0为常数，则称X服从参数为μ,σ的正态分布，记作X ～N (μ,σ²)。正态分布的分布函数为

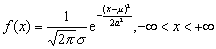
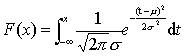
若一个随机变量X的分布函数是正态分布，也称X是一个正态变量。
正态分布是概率论中最重要的一个分布，德国数学家高斯在研究误差理论时曾用它来刻划误差，因而在许多场合也把此分布称为高斯分布。许多实际问题中的变量，如测量误差、射出时弹着点与靶心的距离、热力学中理想气体的分子速度、某地区成年男子身高等，经验表明都服从正态分布。由理论研究表明，若一个变量受到大量微小的、独立的随机因素的影响，则这个变量一般是正态变量。
正态分布的概率密度函数具有下列性质：
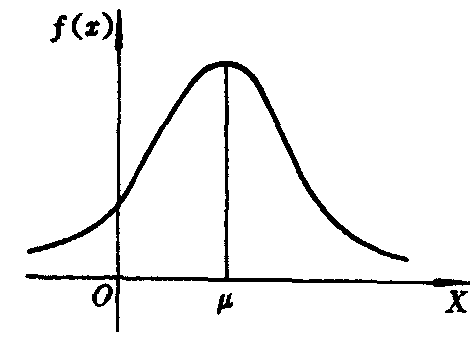
❶在直角坐标系内，f (x)的图形呈钟型，以X轴为水平渐近线。

❷密度分布曲线关于直线x=μ对称，即

f (μ+x) =f (μ-x)。

❸在x=μ时，取到最大值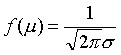在x=μ±σ处图象有拐点。

❹若σ固定，改变μ的值，则f (x)的图形沿着X轴移动，而不改变其形状。若μ固定，改变σ的值，由式子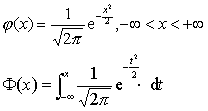可知，σ越小时，图形变得越陡，因而X落在μ处附近的概率越大；反之，当σ的值增大时，曲线将变得平坦。
正态分布的概率密度f (x)与分布函数F (x)的图形如下。

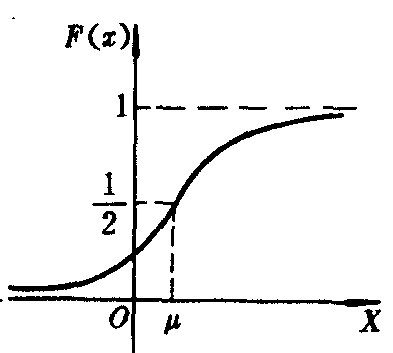
正态分布zheng tai fenbu

又称常态分布、高斯分布。随机变量的一种重要的、应用最多的分布。其数学公式为：

式中e为自然对数的底，μ为平均值，σ为标准差，x为随机变量的取值。最初为德·毛佛尔(De·Moivne)发现，德国数学家高斯(C.F.Gauss)等对其推导做过很大贡献。正态分布曲线有以下特点：曲线呈钟形且左右对称，拐点在μ±σ处，曲线与横坐标所包围的面积为1。曲线随σ大小变化，当μ=0,σ=1时，正态曲线高度适中，称标准正态分布。当σ<1时，曲线高狭，当σ>1时，曲线低阔。有编制好的正态分布表供应用。

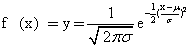
正态分布Zhengtai fenbu

一种重要的连续型随机变量的概率分布，其数学表达式为

式中 π是圆周率3.14159…； e是自然对数的底2.71828…；x为随机变量取值，-∞

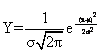
正态分布

又称“高斯分布”。一种最常见、最重要的概率分布。如果一个量受到许多相互独立的随机因素的影响，而每个个别因素的影响都不起决定性作用，那么这个量就近似地服从正态分布。它的分布函数形式为：

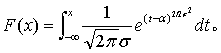
正态分布normal distribution

亦称常态分布或高斯分布。是频数分布中最重要和最常见的一种。是以均数为中心，左右两侧对称，靠近均数频数较多，离均数越远频数越少，形成一个中间多两侧逐渐减少的对称的分布。

正态分布

亦称“高斯分布”。一组测定值中，各测定值的频率分布规律之一。在对某一测试对象进行多次测试时，测得数值在一定范围内波动，其中接近平均值的数值占多数，大于和小于平均值的频率近乎一样，远离平均值的占少数。这种分布规律称为正态分布。用图线表示称为正态分布曲线。正态分布的概率密度函数为：

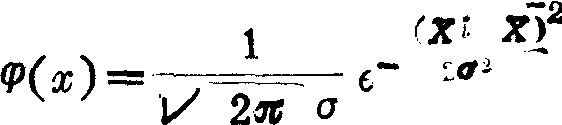
(其中 -∞0),

(x)——在x值处的概率密度；
xi——某次观察值；
——观察值的平均值；
π——圆周率；
σ——标准离差；
e——自然对数的底。
实际测试结果会与上述函数曲线有些出入，但其基本形式相同。观测次数越多越接近上述函数曲线。由函数关系可看出曲线为一对称线，并由和σ所决定。值决定了曲线的高峰位置，决定了峰值的大小和曲线的陡度，σ越小曲线越瘦，表示测试值离散度小(若用来抽查产品时，则表示产品的质量较稳定),σ越大则曲线越胖，说明测试值离散度大。曲线两头逐渐接近X轴，但不相交，说明极大的正误差与负误差的概率非常小。如以曲线和横坐标间的总面积表示概率并等于100%，则±σ范围内的概率为68.2%,±2σ范围内的几率为95.44%,±3σ范围内的概率为99.73%。正态分布是非离散型随机变量的一个最重要、最基本的分布规律，已广泛用于产品抽检、产品质量指标制订，混凝土设计和施工工艺的选择等。

正态分布normal distribution

是一种最常见也是最重要的随机变量的分布形式，也称“高斯分布”或“拉普拉斯分布”。当随机变量x的密度函数形式为：

，称x的分布为正态分布，记为X～N (μ,δ²⁾，密度函数中μ和δ²分别是X的数学期望和方差。正态分布密度函数的图形如下：

正态分布曲线有三个特点：(1)以x=μ为中心左右对称；(2)在x=μ+θ和x=μ-θ处，曲线有两个拐点；(3)以全曲线与X轴所围面积等于1。当μ=0,δ²＝1时，称X服从标准正态分布，记为X～N(0,1)，对于非标准正态分布的随机量X，可以做如下变换，Z=x-μ/δ使Z服从标准正态分布。

正态分布Normal Distribution

亦称“高斯分布”。描述随机现象的一种最常见的分布。用函数表示为：f(x)=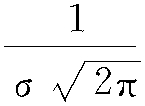e^{-(x-μ)2/(2σ)2}。此函数为正态分布的密度函数，其中，μ是数学期望，参数σ是根方差。当μ=0和σ=1时，相应的正态分布称为标准正态分布。一般地，如果研究的某个量是被彼此相互独立的大量偶然因素所影响的，并且其中每一个因素在总的影响中只起很小的作用，那么这个总的影响所引起的数量上的变化，就近似地服从正态分布。

正态分布

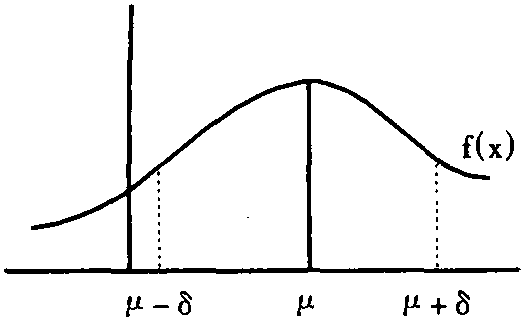
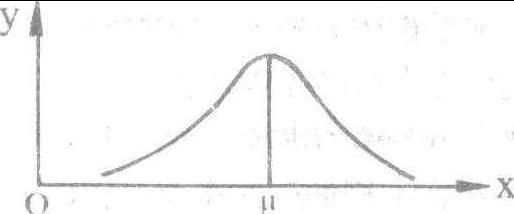
随机变量的一种重要分布。其特征是：对一个变量的样本观测值来说，与其平均值比较接近的观测值出现的次数较多，与其平均值相差较大的观测值出现的次数较少，样本观测值的分布以其平均值为中心，左右对称，像一座古钟（如图）。许多随机变量近似地服从正态分布。

正态分布

又称常态分布或高斯分布。描述连续型随机变量的概率密度函数的一种分布。若连续型随机变量x的概率密度函数为：

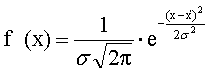
(-∞ 则称x服从以、σ>0为参数的正态分布。式中，为正态分布的平均数，σ²为该变量的方差，e为自然对数的底数。正态分布的分布函数为：

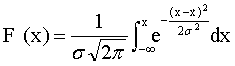
服从正态分布的随机变量简称为正态变量。正态分布具有下列特征： (1) 它所呈现的分布状况均有一中间数值 (), 而观测的变量值多集中于中间数值附近，使变量值的次数分布呈现中间大、两头小的状况； (2)函数f (x)在x=时达到最大值，且左右两侧对称于x=; (3)函数f (x)的值随x的值向左右两端远离而减小，当x的值趋近正负无穷大时，f (x)的值趋近于0; (4)根据函数f (x)所描绘的曲线叫做正态分布曲线，该曲线和x轴所围成的区域总面积为1，即概率积分f(x)dx=1。
正态分布曲线可图示如下：

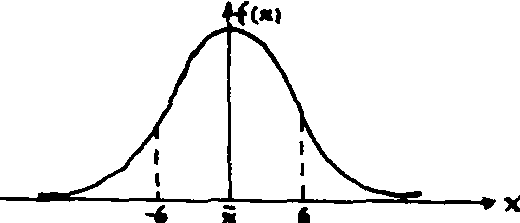
由于正态分布曲线形状犹如一口倒扣的古钟，故又称为“钟形曲线”。正态分布的应用范围很广泛。一般说来，若影响若一数量指标的因素很多，而每一个因素所起的作用都不太大，则这个指标就服从正态分布。 通常将参数为和σ的正态分布记作N (,σ)，特别当＝0,σ=1时，这种正态分布称为标准正态分布，记作N (0,1)。其密度函数为f(z)=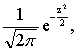借用标准正态分布密度函数的计算公式，并对一般的正态变量x按公式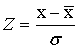加以标准化，使x变为标准正态变量Z，然后根据《标准正态分布表》进行查索，就能得到所需要的概率积分值.

正态分布

正态分布又称高斯分布，是一种最重要的连续型分布。它是以均数为中心呈对称的钟型分布，如图1所示。早在1733年A. de Moivre首先提出这种分布的方程，他以此作为二项分布的极限形式。至19世纪初期，德国数学家C. F. Gauss与法国数学家P.S.de Laplace分别加以发展，用于研究观察误差的分布，但他们过分强调一切自然现象均服从正态分布。经半世纪之后K.Pearson论证，正态分布只是自然现象分布的一种形式。然而正态分布仍不失其重要意义。在医学科研中应用很广，也是许多统计方法建立的基础。
密度函数及其图形 正态分布的密度函数，即正态曲线的方程为

式中f(X)为与X对应的正态曲线的纵坐标高度。已知总体均数μ与总体标准差σ，就能按式(1)描绘出正态曲线，如图1(横轴下μ两侧数值前均省去μ)，其分布函数为

式中F(X)为正态曲线下自-∞到X的面积。标准正态分布 如使式(2)右侧作变量变换：

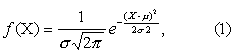
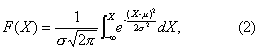
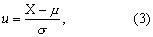
式中u为标准正态变量，如此，则正态分布即可转化成标准正态分布。反映其纵坐标高度的密度函数成为

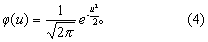
反映其面积的分布函数为

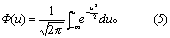
图形如图2。
正态分布常简记为N(μ,σ2)，标准正态分布常简记为N(0,1)。标准正态变量的取值称为标准正态（离）差。性质
(1)正态分布的均数为μ，标准正态分布的均数为0。
(2) 正态分布的方差为σ2，标准正态分布的方差为1。
(3) 正态分布的三阶中心矩（即正态分布的偏度系数）为0。
(4)正态分布的四阶中心矩（即正态分布的峰度系数）为3σ4。
(5)面积规律。在正态曲线下，X轴上μ左右两侧各1σ 间的面积为68.27%，各 1.96σ 间的面积为95.00%，各2.58σ间的面积为99.00%，见图1。

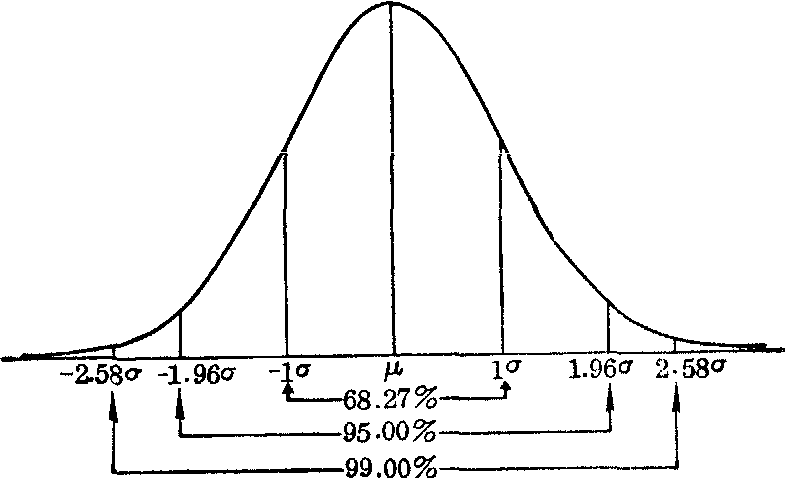
图1 正态曲线及其面积分布

当X、μ与σ已知时，即可按式(3)求得u，按式(4)求得标准正态曲线的纵坐标高度φ(u)，按式(5)求得自-∞到u的面积Φ(u)，见图2。

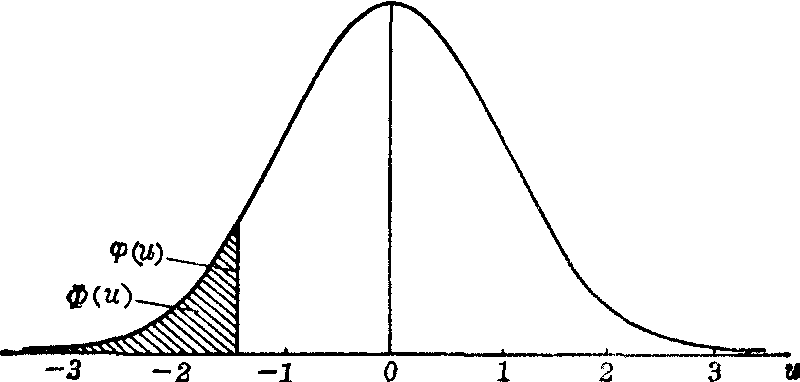
图2 标准正态曲线的纵坐标与面积

已知u，求φ(u)与Φ(u)均有统计表可查，φ(u)值表见条目“正态曲线拟合”。求标准正态分布函数Φ(u)值可查表1。如u=-1.96时，查表1得 Φ(-1.96)=0.0250；但u为正时，如u=1.96，表中查不到，须用倒推法，即Φ(1.96)=1-Φ(-1.96)=1-0.0250=0.9750.

表1 标准正态分布曲线下的面积
[本表为自-∞到-u的面积Φ(-u),Φ(u)=1-Φ(-u)]

u	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
-3.0 -2.9 -2.8 -2.7 -2.6 -2.5	.0013 .0019 .0026 .0035 .0047 .0062	.0013 .0018 .0025 .0034 .0045 .0060	.0013 .0018 .0024 .0033 .0044 .0059	.0012 .0017 .0023 .0032 .0043 .0057	.0012 .0016 .0023 .0031 .0041 .0055	.0011 .0016 .0022 .0030 .0040 .0054	.0011 .0015 .0021 .0029 .0039 .0052	.0011 .0015 .0021 .0028 .0038 .0051	.0010 .0014 .0020 .0027 .0037 .0049	.0010 .0014 .0019 .0026 .0036 .0048
-2.4 -2.3 -2.2 -2.1 -2.0	.0082 .0107 .0139 .0179 .0228	.0080 .0104 .0136 .0174 .0222	.0078 .0102 .0132 .0170 .0217	.0075 .0099 .0129 .0166 .0212	.0073 .0096 .0125 .0162 .0207	.0071 .0094 .0122 .0158 .0202	.0069 .0091 .0119 .0154 .0197	.0068 .0089 .0116 .0150 .0192	.0066 .0087 .0113 .0146 .0188	.0064 .0084 .0110 .0143 .0183
-1.9 -1.8 -1.7 -1.6 -1.5	.0287 .0359 .0446 .0548 .0668	.0281 .0351 .0436 .0537 .0655	.0274 .0344 .0427 .0526 .0643	.0268 .0336 .0418 .0516 .0630	.0262 .0329 .0409 .0505 .0618	.0256 .0322 .0401 .0495 .0606	.0250 .0314 .0392 .0485 .0594	.0244 .0307 .0384 .0475 .0582	.0239 .0301 .0375 .0465 .0571	.0233 .0294 .0367 .0455 .0559
-1.4 -1.3 -1.2 -1.1 -1.0	.0808 .0968 .1151 .1357 .1587	.0793 .0951 .1131 .1335 .1562	.0778 .0934 .1112 .1314 .1539	.0764 .0918 .1093 .1292 .1515	.0749 .0901 .1075 .1271 .1492	.0735 .0885 .1056 .1251 .1469	.0721 .0869 .1038 .1230 .1446	.0708 .0853 .1020 .1210 .1423	.0694 .0838 .1003 .1190 .1401	.0681 .0823 .0985 .1170 .1379
-0.9 -0.8 -0.7 -0.6 -0.5	.1841 .2119 .2420 .2743 .3085	.1814 .2090 .2389 .2709 .3050	.1788 .2061 .2358 .2676 .3015	.1762 .2033 .2327 .2643 .2981	.1736 .2005 .2296 .2611 .2946	.1711 .1977 .2266 .2578 .2912	.1685 .1949 .2236 .2546 .2877	.1660 .1922 .2206 .2514 .2843	.1635 .1894 .2177 .2483 .2810	.1611 .1867 .2148 .2451 .2776
-0.4 -0.3 -0.2 -0.1 -0.0	.3446 .3821 .4207 .4602 .5000	.3409 .3783 .4168 .4562 .4960	.3372 .3745 .4129 .4522 .4920	.3336 .3707 .4090 .4483 .4880	.3300 .3669 .4052 .4443 .4840	.3264 .3632 .4013 .4404 .4801	.3228 .3594 .3974 .4364 .4761	.3192 .3557 .3936 .4325 .4721	.3156 .3520 .3897 .4286 .4681	.3121 .3483 .3859 .4247 .4641

本表按式(5)算得。
标准正态分布的分位数 标准正态曲线下，双侧尾部的面积P(2)或单侧尾部的面积P(1)为指定值α时，横轴上相应的u值记为uα，这就是u的分位数。P(2)、P(1)均可按式(6)求得。

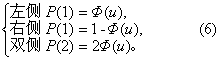
这些数值有u界值表可查，兹节录部分常用者如表2。例如，当α=0.05时，双侧u0.05=1.960，单侧u0.05=1.6449≐1.645。

表2 标准正态分布的分位数简表(u界值表)

P(1): P(2):	0.25 0.50	0.10 0.20	0.05 0.10	0.025 0.05	0.01 0.02	0.005 0.01
u	0.6745	1.2816	1.6449	1.9600	2.3263	2.5758

用途 正态分布的用途很广，如
(1)众多微小且独立的随机因素（其中没有一个是主导的）影响的总结果，一般表现为正态分布（中心极限定理）。如随机误差的分布，某些生理现象的频率分布等，都可认为是正态分布。
(2)某些统计量的抽样分布，如x2、t与F分布都是在正态分布的基础上推导出来的。
(3)某些分布，如二项分布、Poisson分布、t分布等的极限为正态分布。
(4) u检验。以u作为统计量的假设检验称为u检验，它是最常用的一种检验方法。
(5)服从正态分布资料的正常值范围估计，半数效量的计算，质量控制图的绘制等。

正态分布

又称“常态分布”、“机率曲线”等。是人们通过考察自然和社会的各种各样的随机现象分布时总结出来的一种描述连续型随机变量的概率密度的分布模型。正态分布是概率论中一种最重要的分布，它表明，大量随机现象的分布总是围绕在它的平均数两侧的，越偏离到两个极端的分布越少，正偏负偏是对称的。正态分布可以用一条“中间多、两头少、左右对称”的钟形曲线来表示，（参见下图）。其数学公式为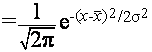：：。其中，x为变项的数值，f(x)为变项值的次数，σ为该变项的标准差，π为圆周率，e为自然对数的底数，为总体各变项的算术平均值。

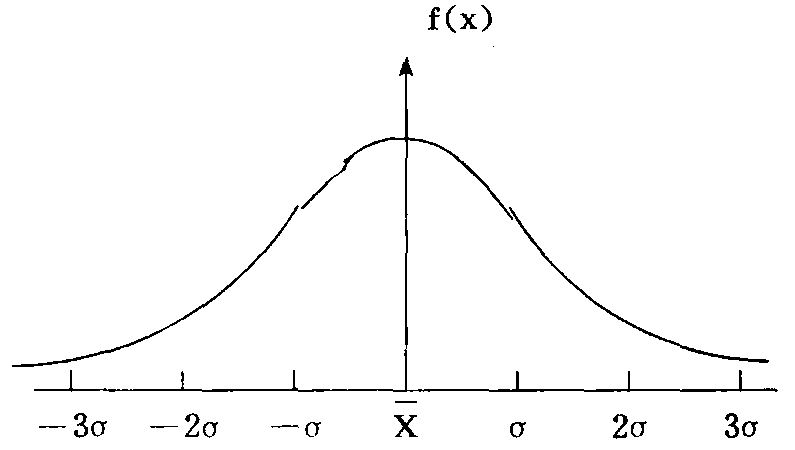
正态曲线

由图可知，舆论研究发现尽管舆论调查对人们意见、态度的测定会受到各种主客观因素的影响而使测量结果不完全相同，但每一次的态度测定值都会相当集中地围绕一个中心点（所有测定值的算术平均值）而呈正态分布。这里所谓的“集中”是有规律可循的，经计算，如果以为中点，左右对称量取1个σ(σ是组成正态分布变量的标准差)的范围，那么，所有可能的态度测定值将有68.27%的取值落在这一范围内；有94.45%的测定值将在以为中点，左右两个σ的范围内；有99.73%测定值将落在以为中点，左右3个σ的范围内。

正态分布

描述概率论中随机现象的一种最常见最重要的理论分布，是一种由二项分配演变而来的连续分配。其次数分配可用称为正态分布曲线的曲线来表示。此曲线周边是一条中央高，两边逐渐下降低平，左右对称，並延伸成钟形。这条曲线与横轴所围成的面积等于1。这种分布又叫常态分布、或称高斯分布。这种曲线又称常态分布曲线、概率曲线或高斯曲线。其曲线方程为：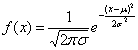

式中： x为随机变量(-∞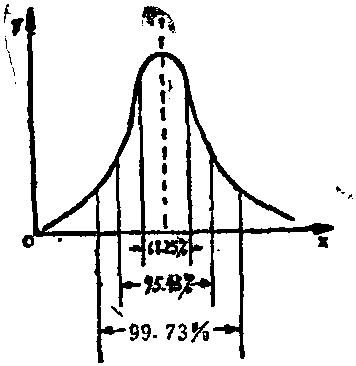

正态分布normal distribution

亦称“高斯分布”或“拉普拉斯分布”。其概率密度函数为

取y=f(x)作图，可描出正态分布的曲线，该曲线有下列特性：
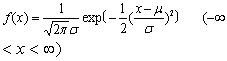
(1)为单峰对称曲线，对称轴是x=μ;
(2)在x=μ±σ处有拐点；
(3)以全曲线与x轴所围面积等于1。该分布期望值E(x)=μ，方差D(x)=σ²，偏度γ₁＝μ₃/σ³＝0，峰度γ₂＝μ₄/σ⁴-3=0，矩母函数
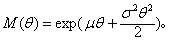
正态分布是最常见的也是最重要的一种分布。不少社会现象、自然技术现象的分布与之相近。在一般假定下，它是n个独立随机变量之和且当n充分大时的极限分布。

正态分布

亦称“常态分布”、“高斯分布”。由德国数学家高斯首先发现。在分配数列中，各组次数逐渐增多，到数列中央后，再逐渐减少。其密度函数为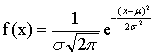：　(-∞ 其一般图形为：

从图形可以看出，正态分布有以下特点： (1) 正态分布所形成的曲线，为单峰钟形对称曲线，对称轴为x=μ。(2) 正态分布由均值μ和标准差σ来确定。μ确定曲线顶峰位置，σ确定曲线的形状。次数分配越分散，σ值越大，则曲线越平坦； 次数分配越集中，σ值越小，则曲线越窄陡。(3) 若以全曲线与x轴所围成的面积作为1; 则在μ±σ范围内的面积为0.6827; 在μ±2σ范围内的面积为0.9545; 在μ±3σ范围内的面积为0.9973。这些已编有正态分布表可供查阅。在实际生活中，许多变量的分配接近于正态分布，如农产品的单位面积产量。数理统计证明，在抽样调查中，当样本数目足够多时，样本平均数的分布服从正态分布，这就为抽样推断提供了理论依据。

正态分布normal distribution

亦称“常态分布”、“高斯分布”、“常态曲线”等。是统计中最重要的分布。德国数学家高斯(Gauss, C.F.)首先发现，正态分布指示了自然和社会多种随机现象分布的一种分布规律。正态分布在心理测验上的应用主要表现在以下几个方面： (1)化某级评定为测量数据。(2)确定测验题目的难度。(3)在能力分组或等级评定时确定人数。正态分布曲线呈中间高，两侧对称平滑下降的钟型曲线。正态分布的计算公式为：

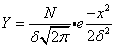
式中Y为纵线高度；N为总次数；δ为分布的标准差；e为自然对数之底，2.71828;x为测量值与平均数之差，即(X-)。由于正态分布曲线下的面积总保持为1, 因此，当δ不相同时， 曲线的形状也有所不同，δ愈小，分布求集中在平均数附近； δ愈大，分布则愈平坦。

正态分布normal distribution

亦称“常态分布”、“常态分配”、“高斯分布”。与“偏态分布”相对。分布曲线左右对称的数据次数分布。连续随机变量概率分布的一种。是统计理论和应用中最重要的一种理论分布。由英国数学家棣莫佛(Abraham de Moivre, 1667—1754)于1733年发现。特征为以平均数为对称轴，左右对称，平均数为最高点，曲线下面积为1，以平均数和方差的不同而不同。所有正态分布经过标准化后，可以转化为标准正态分布。自然界、人类社会中大量现象均按正态分布，如能力的高低，学生成绩的好坏，人们的社会态度，行为表现以及身高、体重等身体状态都属于正态分布。

正态分布

亦称“常态分布”、“常态分配”。与“偏态分布”相对。分布曲线左右对称的数据次数分布。连续随机变量概率分布的一种。统计理论和应用中最重要的一种理论分布。由棣·莫弗1733年发现，由于德国数学家高斯等的贡献，有时又叫高斯分布。正态分布的特征为以平均数为对称轴，左右对称，平均数为最高点，曲线下面积为1，以平均数和方差的不同而不同的一族分布。所有正态分布经过标准化后，可以转化为标准正态分布(平均数为0，方差为1的分布)。