椭圆抛物面
椭圆抛物面tuoyuan paowumian
在空间直角坐标系下,由三元二次方程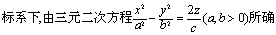 (a,b>0)所确定的曲面. 这个方程叫做它的标准方程. 椭圆抛物面的性质如下:
(a,b>0)所确定的曲面. 这个方程叫做它的标准方程. 椭圆抛物面的性质如下:
❶对称性 曲面关于YZ面、ZX面对称,这两个平面叫做主平面;关于Z轴对称,Z轴叫做主轴;关于原点则不对称.
❷截距 在坐标轴上的截距都是零,因此曲面过原点,并将原点叫做端点或顶点.
❸截部 在YZ面、ZX面上的截部分别是抛物线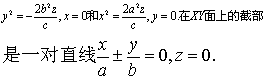 x=0和
x=0和 y=0,在XY面上的截部为原点.
y=0,在XY面上的截部为原点.

❹轮廓线 在z=w上的轮廓线是
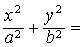
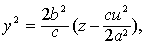 x=u. 当u变化时,表示顶点在
x=u. 当u变化时,表示顶点在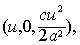 焦参数为
焦参数为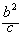 的全等抛物线.在y=v上的轮廓线也是全等抛物线. c> 0时,曲面的形状见图.
的全等抛物线.在y=v上的轮廓线也是全等抛物线. c> 0时,曲面的形状见图.其它两个椭圆抛物面的标准方程是
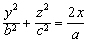 和
和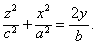
☚ 双叶双曲面 双曲抛物面 ☛
- 组织设计及组织结构是什么意思
- 组织设计基本理论是什么意思
- 组织设计教学程序的技能是什么意思
- 组织诊断是什么意思
- 组织课外学科小组活动的技能是什么意思
- 组织课外科技活动小组的技能是什么意思
- 组织起来是什么意思
- 组织越狱罪是什么意思
- 组织路线是什么意思
- 组织辅导是什么意思
- 组织运用是什么意思
- 组织运送它人偷越国(边)境罪是什么意思
- 组织进攻的后卫是什么意思
- 组织进攻队员是什么意思
- 组织速测诊断是什么意思
- 组织部是什么意思
- 组织部新来的青年人是什么意思
- 组织部门的职责是什么意思
- 组织配型试验是什么意思
- 组织鉴定是什么意思
- 组织错综是什么意思
- 组织间桥是什么意思
- 组织集团是什么意思
- 组织驱动型模式是什么意思
- 组织驻军参加重大活动是什么意思
- 组绣是什么意思
- 组绶是什么意思
- 组编是什么意思
- 组缨是什么意思
- 组群理论是什么意思
- 组胺是什么意思
- 组胺受体是什么意思
- 组舞是什么意思
- 组蛋白是什么意思
- 组蛋白抗体是什么意思
- 组装是什么意思
- 组装件是什么意思
- 组装式制冷设备是什么意思
- 组装机是什么意思
- 组词是什么意思
- 组词配合法是什么意思
- 组诗是什么意思
- 组谜是什么意思
- 组距是什么意思
- 组距式变量数列是什么意思
- 组距数列是什么意思
- 组配是什么意思
- 组配复分号是什么意思
- 组配标引是什么意思
- 组配检索是什么意思
- 组配程度检索是什么意思
- 组配规则是什么意思
- 组锯法是什么意思
- 组长是什么意思
- 组间比较是什么意思
- 组间设计是什么意思
- 组阁是什么意思
- 组队是什么意思
- 组限是什么意思
- 组雕是什么意思