瓦尔拉斯需求

---

消费者效用最大化问题可用下式表示：

Max U(x)

x≥0

s．t．p·x≤w

在效用最大化问题中，在每一价格－财富点(p，w)》0，最优消费矢量由x(p，w)∈R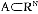表示，并被称为瓦尔拉斯(或正常的或市场的)需求效应，当x(p，w)对于所有(p，w)为单值时，x(p，w)∈R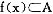被称为瓦尔拉斯(或正常的或市场的)需求函数。

假设U(·)是一连续的效用函数，它代表一个定义在消费集x=R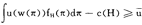的局部非满足偏好关系≥。则瓦尔拉斯需求效应x(p，w)具有下列特征：

(1)0次同质性：对于任意p、w及α＞0，x(α p，α w)=x(p，w)

(2)瓦尔拉斯定律：对于所有的x∈x(p，w)，p·x=w

(3)凸性或惟一性：如果偏好≥具有凸性，则U(·)为半凹，从而x(p，w)为一凸集；更进一步，如果≥为严格凸性，则U(·)为严格半凹，(p，w)只有单个元素。