循环序列相关系数的分布

---

序列相关是许多动态模型随机扰动的重要特性，在许多学科中，(如时间序列分析、经济计量学等)都对序列相关有专门的讨论。

要检验某一模型中随机扰动有无序列相关性，首先要知道序列相关系数的分布，或了解其分布的某些特征等。因此，研究序列相关系数的分布就显得十分重要。

设(Z，Z₂，…，Z_n)为取自随机扰动Z_t的一个时间序列样本，定义第1(落后1步的)序列方差为：

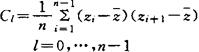
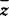为所观测序列的样本均值．

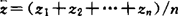于是得到第1(落后1步的)序列相关系数：

γ_l=c_l／c_o

在进行分布理论的研究中，即使在扰动z₁为标准正态白声(独立同分布)的假设下，也不可能求得γ₁的分布的明显形式。

但是如果考虑循环序列相关系数，分布问题便可以解决。

设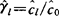

此处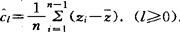．而循环的定义为z_l+n=z_l．

在对z_t为标准正态白声的假设之下，当l=1时(落后一步)有：

其中：

λi=cos(2πi／n) i=0，1，2，…，n－1

v_i～x²(2)． v～x²(1)

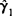的分布函数为：

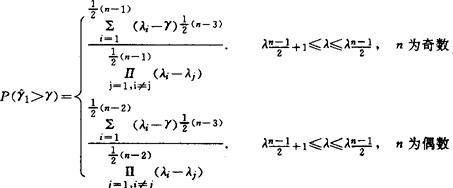
上述结果是由安德森(R．L Anderson)于1942年给出的，通常称为安德森分布(R．L Anderson)．由此我们可得对原假设显著性的单侧或双侧检验。但杜宾(Dubin)和沃森(Watson)在1971年曾指出，其中的主要结果早在1863年已由阿比(Abbe)得到。

一般情况下，R．L Anderson有如下结果：对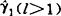当l与n无公约数时：

λ_k=cos(2kπlk／n)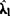，的分布同l=1，如果l与n有公约数，分布的函数形式可能改变。

R．L Anderson在推导分布时所用的技巧是求一循环矩阵的行列式值，并用联合分布求边缘分布。

对于一般情况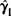分布的具体结果，采用分解循环矩阵和特征函数的方法推导了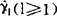的分布函数。

迪克森(Dixon，1944)通过对(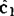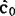，)的特征函数：

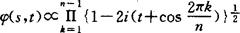
进行近似，使得：

于是得到其前n阶矩与下述分布：

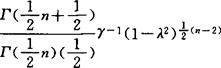
相同。于是可得上述R．L．Anderson分布的近似表达式，也就是说，循环序列相关系数的分布近似于从标准正态总体中抽出容量为n+2的样本的普通相关系数平方的分布。

在推导循环序列相关系数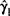分布的过程中，所用的重要技巧是对循环矩阵复数域的求行列式值或酉阵对角化分解，而序列相关系数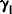却不能由循环矩阵表示，因而不可能用此法求其分布。

有关循环序列相关系数分布的进一步讨论可从两方面展开：首先是非循环情形，即对序列相关系数的讨论，这方面的研究很多，文献资料也很丰富。但这已超出本条目的内容。

其次，是在非标准状态下，循环序列相关系数及其联合分布的讨论。几十年来，有关这方面的讨论很少，零星的几篇文献讨论的也比较肤浅，结果并不理想。

特别是近些年来循环序列相关系数似乎要被人们遗忘。这也许是新的热门的统计学课题不断涌出，吸引了人们的注意，另一方面，是因为用现有的方法对循环序列相关系数分布研究很繁琐，是否用新的数学工具进行研究是今后的新课题。

。【参考文献】：

1 Anderson RL. Ann Math Statistics, 1942,13:1～13

2 Dixon W J. Ann Math Stat,1944,15:119

3 Durbin J, et al. Testing for Serial Corrlation in the least Squares regression I . Ⅱ. Ⅲ Biometrika, 1950, 37;4～9; 1951,38,159;l971,58,(1)

4 Watson GS, et al. Ann Math Stat,1951,22:46

5 Watson G S. On the Joint distribution of Circular Serial correlation coefficients. Biome treka,1956,43:161

6 Vif Grenander, et al. Statistical Analysis of Stationary Time Serial. John & Sons. 1957

7 Kendal M. The Advanced Theory of Statistics, 3. Butler & Tamner Ltd, 3

8 朱世斌．河南师范大学学报，1988，4：17～25

(河南师范大学朱世斌撰)