阶梯光栅jieti guangshan

介质排列得象阶梯形的光栅。阶梯光栅又称迈克耳孙梯，是迈克耳孙在1898年首先设计出来的，而后威廉斯等人进行了改进。图1是一个透射式阶梯光栅，它由若干块厚度都是t、折射率都是n的玻璃板叠合而成，后面的一块都比前一块短一些，因而形成阶梯。设平行光垂直地自左端射入，则在右端衍射角θ的方向上，当θ不大时，相邻两阶梯的光程差为(n-1)t+θd，因而产生相应的相位差。d是阶梯高度，这阶梯相当于单缝。阶梯光栅可获得高分辨本领的强光谱。它和普通的刻痕光栅都可获得高分辨本领，但原理有所不同。根据理论分析，光栅的分辨本领R= KN，普通刻痕光栅中，光谱级数K不大，而单缝总数N很大，以获得大的R；在阶梯光栅中，N不大(20～40)，但以增大K的办法来增大R。由上述光程差公式可见，在θ不大时，透射式阶梯光栅的光栅方程为(n-1)t+_dθ=Kλ。若t=1厘米，d=0.1厘米，θ=0,n=1.5，则对λ=500纳米的绿光，K=10⁴；若N=30，则R=3×10⁵，此时可分辨的最小波长差为△λ=1.7×10^-3纳米，可见K与R都达到了刻痕光栅难以达到的数值。而且由于d远大于λ，相当于单缝衍射中央条纹很窄，光能集中，增加了谱线亮度。不过高级次的衍射光谱容易发生重叠，故阶梯光栅最适于研究光谱的精细结构。先用其它方法分出一条窄波段，然后用阶梯光栅来研究它。阶梯光栅也有反射式的，如图2所示。当θ角不大时其光栅方程为2t-dθ=Kλ。在同样t、d的情况下，反射式阶梯光栅的分辨本领约为透射式的4倍，阶梯光栅由于制造困难，又只适用于光谱的高分辨，故到现在还没有被广泛使用。

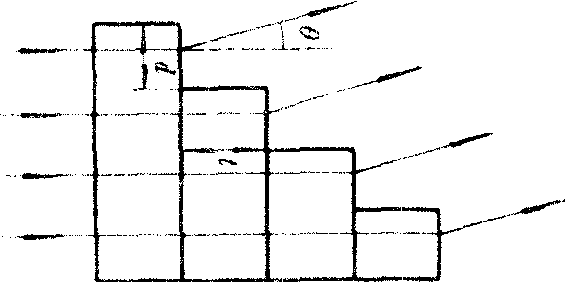
图 1

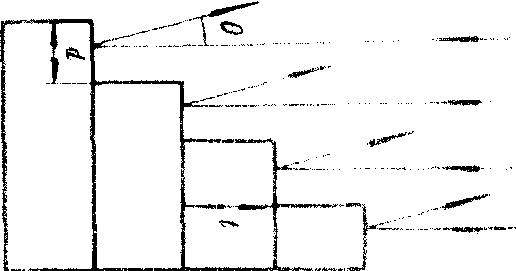
图 2