运输模型

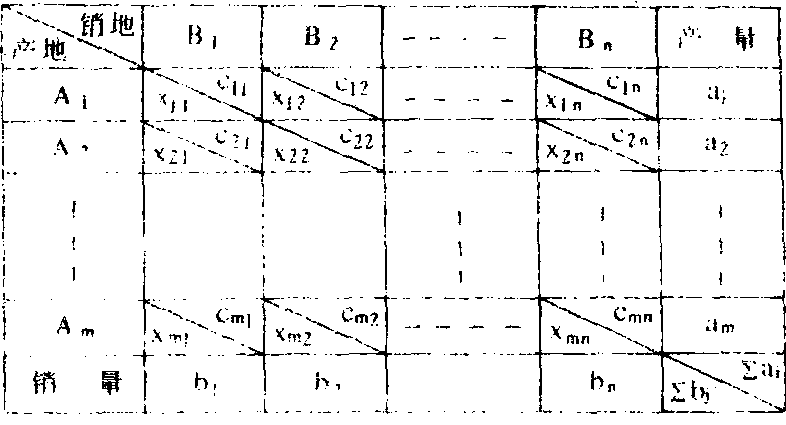
在生产经营活动中，如何确定从某几个产地购货，又分别向另外几个销地送货的运输量，以使总调运费最小的问题的数学模型。研究这类问题的实际意义，远不止解决货物调运的最优化，还有其他方面的应用，称它为“运输模型”是由于习惯和方便的缘故。运输模型的建模条件是： 有m个生产地点 （产地），可以供应某种同类物资，以Ai表示产地，ai表示产地Ai的可供应数量 （产量）,i=1 …m; 有n个消费地点 （销地） 需要该种物资，用Bj表示销地，bj表示销地Bj的需要量 （销量）,j=1…n，从产地Ai到销地Bj的单位货物运价为Cij。如何作出合理的调运安排，使总的运输成本最低。在上述问题中。 若m个产地的产量总和与n个销地销量的总和相等时， 即＝, 称为产销平衡的运输问题，产销平衡运输问题的数学模型一般形式为：

这个模型亦可用下面的矩阵表格表示：

求解运输问题可以利用上述表格直接进行计算，称表上作业法。求解某些运输问题的另一种方法是由我国运筹学研究人员总结出来的图上作业法。在运输图上直接进行运算的方法，称图上作业法。
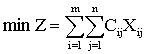
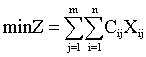
除了产销平衡的运输问题外，在实际问题中还有几类其他问题：
(1) 产大于销运输问题， 即>时， 这类运输问题模型为：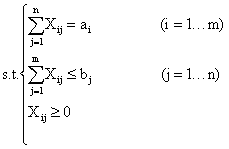

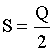
(2)销大于产运输问题， 即<时， 这类运输问题模型为：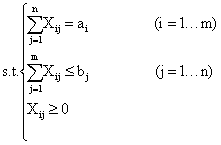

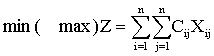
(3) 转运问题： 上述运输问题，货物的流动总是从一个产地到另一个销地。实际运输问题中，还包括从产地到产地、销地到销地，甚至销地到产地货物流动的运输问题。这就是转运问题。
以上这三类运输问题都可以通过适当的数学处理，用表上作业法进行求解。