词语“西摩松线”的读音、偏旁部首、笔画笔顺、组词造句、释义及意思翻译-中英文字词句释义及详细解析-文网

网站首页词典首页

字词	西摩松线
类别	中英文字词句释义及详细解析
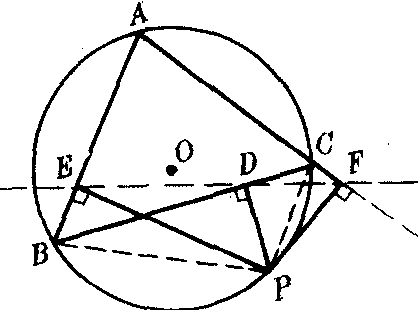
释义	西摩松线西摩松线ximosongxian 从三角形外接圆上任意一点作三边所在直线的垂线，其三垂足所在的直线叫西摩松线.如图，若P为△ABC外接圆上任意一点，PD⊥BC于D,PE⊥AB于E,PF⊥CA于F，则D,E,F共线. 连结ED,FD,CP,BP，由B,P,D,E四点共圆可知 ∠EDB=∠EPB, 同理，∠FDC=∠FPC.又∠FCP=∠EBP（圆内接四边形一个外角等于它的内对角）.故∠EPB=∠FPC.所以∠EDB=∠FDC.则E,D,F三点共线.这个证明是西摩松最先给出的，因此把EDF叫做西摩松线. ☚ 波罗摩笈多定理　帕斯卡定理 ☛ 00012760
随便看	归化族是什么意思归化法是什么意思归化苗民是什么意思归化郡是什么意思归化驻防城是什么意思归十归一是什么意思归华别叶是什么意思归华寺是什么意思归卧是什么意思归卧云庐霜满鬓，十年间、多少愁思。是什么意思归卷类目是什么意思归厚传是什么意思归原是什么意思归原扇存十卷是什么意思归原散是什么意思归去是什么意思归去。是什么意思归去不堪春梦断，烟雨晓，乱山重。是什么意思归去也，且斓斑戏彩，好春长日。是什么意思归去也，幅巾谈笑，卒岁且优游。是什么意思归去也，白云一片愁空外。是什么意思归去争先戴取，倚宝钗双燕。是什么意思归去五株彭泽柳，困来七碗玉川茶。是什么意思归去亦何须，单车渡殽渑。是什么意思归去只愁红日短是什么意思归去和羹未晚，劝行人休摘。是什么意思归去好。是什么意思归去好，人生莫被浮名误。是什么意思归去好，北门夜饮金莲烛。是什么意思归去想娇娆，暗魂销。是什么意思归去懒。是什么意思归去故山，犹带白云封。是什么意思归去晚，任帘栊、深闭未知。是什么意思归去曲是什么意思归去来是什么意思归去来、一曲为君吟，为君寿。是什么意思归去来、一曲仲宣吟，从军乐。是什么意思归去来、莫教子规啼，芳菲歇。是什么意思归去来兮是什么意思归去来兮引是什么意思归去来兮辞是什么意思归去来兮辞(并序)是什么意思归去来兮辞并序是什么意思归去来兮，吾家何在，结茆水际林边。是什么意思归去来兮，忘我忘世。是什么意思归去来兮，田园将芜。胡不归。是什么意思归去来兮，田园将芜胡不归！既自以心为形役，奚惆怅而独悲。悟以是什么意思归去来兮，田园将芜胡不归！既自以心为形役，奚惆怅而独悲！悟已往之不谏，知来者之可追；实迷途其未远，觉今是而昨非。舟遥遥以轻飏，风飘飘而吹衣。问征夫以前路，恨晨光之熹微。乃瞻衡宇，载欣载奔。僮仆欢迎，稚子候门。三径就荒，松菊犹存。携幼入室，有酒盈樽。引壶觞以自酌，眄庭柯以怡颜。倚南窗以寄傲，审容膝之易安。园日涉以成趣，门虽设而常关。策扶老以流憩，时矫首而遐观。云无心以出岫，鸟倦飞而知还。景翳翳以将入，抚孤松而盘桓。归去来兮，请息交以绝游。世与我而相违，复驾言兮焉求！悦亲戚之情话，乐琴书以诮忧。农人告余以春及，将有事于西畴。或命巾车，或棹孤舟。既窈窕以寻壑，亦崎岖而经丘。木欣欣以向荣，泉涓涓而始流。善万物之得时，感吾生之行休。已矣乎，寓形宇内复几时！曷不委心任去留？胡为乎遑遑欲何之？富贵非吾愿，帝乡不可期。怀良辰以孤往，或植杖而耘耔。登东皋以舒啸，临清流而赋诗。聊乘化以归尽，乐夫天命复奚疑！是什么意思归去来兮，长安古道，隐隐断霞残照。是什么意思归去来堂是什么意思归去来辞是什么意思归去来辞图竹刻笔筒是什么意思归去来，田园恐荒芜。是什么意思归去江湖一叶，浩然对影垂竿。是什么意思归去汴桥三鼓月，相思梁苑一枝梅。是什么意思归去祭祀是什么意思归去难是什么意思归参炖母鸡是什么意思归反是什么意思归叟是什么意思

文网收录3541549条中英文词条，其功能与新华字典、现代汉语词典、牛津高阶英汉词典等各类中英文词典类似，基本涵盖了全部常用中英文字词句的读音、释义及用法，是语言学习和写作的有利工具。

西摩松线ximosongxian