保角映射

---

12．2．1 保角映射及其性质

双方单值连续的映射定理：设ω=f(z)是z平面域D内的单值连续函数，如果它又是单叶的，那么D的象Σ仍是一个域，而且反函数z=φ(ω)在Σ内连续。这种双方单值连续的映射称为拓扑映射或同胚映射。

保角映射及其充要条件：如果在域D内任一点z的邻域里函数ω=f(z)的映射满足条件：(i)伸缩率不变；(ii)旋转角不变，并保持角的定向，则称函数ω=f(z)的映射是区域D内的保角映射(保角变换)。ω=f(z)在区域D内是保角映射的充要条件，是f(z)在D内解析且导数f′(z)在域D内处处不等于零。

域D内保角映射f(z)的性质如下：

❶ D内任一无穷小圆周的象在相差一个高阶无穷小的程度内是圆周。

❷ D内两曲线的夹角映射后保持不变。

❸ D内任一域(包括D本身)的象是区域。

❹ 在D内的任一点z处，|f(z)|不能达到极大值，也不能达到极小值。

❺ D内任一点z处都各有一邻域，在此邻域中f(z)是单叶的。

12．2．2 分式线性映射及其性质

分式线性函数

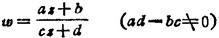
所实现的映射称为分式线性映射(分式线性变换)，其逆映射为

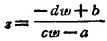
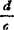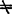也是一个分式线性映射。规定z=－(c0)

对应ω=∞，z=∞(c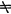0)对应ω=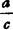。当c=0时，z=∞对应ω=∞，那么分式线性映射确定了一个扩充z平面与扩充ω平面之间的一个一一对应关系。

分式线性映射具有如下性质：

❶ 在扩充平面上处处有保角性。

❷ 在分式线性变换下，圆周仍变为圆周。

❸ 关于圆或直线的对称点映射后仍保持对称性。

❹ 把z平面上任意三点z₁，z₂，z₃分别映射到ω平面上的任意三点ω₁，ω₂，ω₂的分式线性映射是唯一的，即

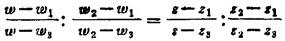
❺ 扩充z平面的任一圆都可以找到一个分式线性映射将它映射到扩充ω平面上的任意一圆。

❻ 在分式线性映射下，四点z₁，z₂，z₃，z₄的交比保持不变．(z₁，z₂，z₃，z₄的交比是)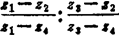

12．2．3 简单分式线性映射

❶ 平移映射 ω=z+c(c为复常数)

把图形平移一个复数c。

❷ 伸缩与旋转映射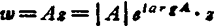

把模以原点为中心伸缩|A|倍，再绕原点O旋转一个角度argA。

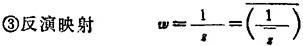
把单位圆内(外)一点映射到圆外(内)一点(这两点同在一条过原点的射线上，且其模互为倒数)，然后再把这个象点映射到它关于实轴的对称点上，

❹ 分式线性映射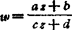

(i)当a、b、c、d都是实数时，z平面的实轴Imz=0映射成ω平面的实轴Imω=0。

(ii)当ad－bc＞0时，把上半z平面Imz＞0映射到上半ω平面Imω＞0。

(iii)当ad－bc＜0时，把上半z平面Imz＞0映射到下半ω平面Imω＜0。