简谐振动的能量jianxie zhendong de nengliang

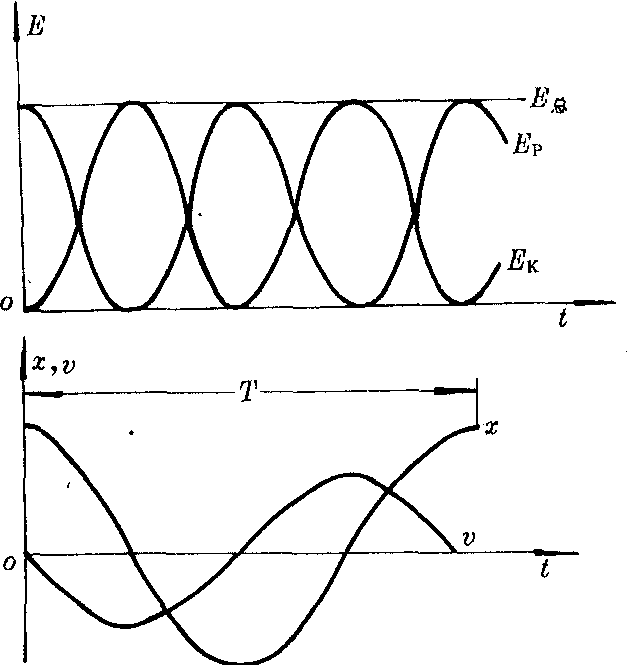
在机械振动中，对于简谐振动，由于作用于振动系统的线性回复力（或力矩）是保守力（或保守力矩），所以简谐振动的机械能是守恒的。以弹簧振子为例，位移为x=正比。由于谐振动的振幅是由初位移和初速度决定的常数，所以谐振动的总能量等于初始时刻外部所给于系统的能量。图中给出了简谐振动(设ᵠ=0)动能、势能和机械能随时间变化的曲线。由图可见，在谐振动过程中，动能和势能相互转换而总能量为一恒量。再与谐振动的位移曲线和速度曲线相比较，则可知振动系统任一振动状态下的动能和势能。当位移最大时，势能达最大值，动能为零。当位移为零时，势能为零，动能达最大值。且可知动能和势能的变化频率均是谐振动的固有频率的两倍。在量子力学中处于与位移平方成正比的一维势场中运动的微观粒子也称为线性谐振子（简称谐振子）。这种量子力学的谐振子的能量与经典谐振子不同，不能连续变化，而只能取满足下式的离散值En=(n+1/2)ħω,(n=0,1,2，…),h为普朗克常数ħ除以2π,ω是圆频率，n取不同的整数时得到谐振子能量的不同能级，谐振子各能级的间隔相同都是hω。当n=0时是谐振子的零点能，也叫谐振子的基态能。n→∞时与经典谐振子没有区别。