极差分析
极差分析
极差又称全距,是一组变量值中最大值与最小值之差,符号为R。极差是一种最简单但较粗略的变异指标,它没有利用全部数据所提供的信息,又易受个别极端值的影响,而对于来自正态总体的小样本,则是一种较有效的变异指标。极差分析可用于参数估计、容许区间估计和假设检验等。参数估计
总体标准差的点估计 如样本来自正态总体,可按式(1)由极差R估计总体标准差σ。
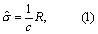
 为总体标准差σ的估计值,与用样本标准差s估计总体标准差相比,用极差估计的相对效率随样本含量增大而渐减。c为系数,随样本含量增加而渐增。均见表1。
为总体标准差σ的估计值,与用样本标准差s估计总体标准差相比,用极差估计的相对效率随样本含量增大而渐减。c为系数,随样本含量增加而渐增。均见表1。表1 由R估计σ用的系数c与相对效率
| 样本含量 | c | 相对效率 |
| 2 4 6 8 10 20 30 40 50 | 1.13 2.06 2.53 2.85 3.08 3.73 4.08 4.33 4.50 | 1.000 0.975 0.933 0.890 0.850 0.700 0.604 0.536 0.490 |
摘自 Snedecor GW: Statistical Methods,fifth edi-tion,p 38,The Iowa State College Press,1959
为了提高估计的准确性,尤其当总例数较多时,可先将变量值随机分成k个例数相等的组,分别求出各组的极差,再用平均极差R按式(2)估计总体标准差。
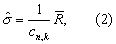
总体均数的区间估计 可按式(3)及式(4)计算由极差估计总体均数的可信区间Cl。
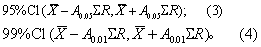
表2 由R估计σ的系数cn,k
| 组数 k | 每 组 例 数,n | ||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 2 3 4 5 | 1.41 1.28 1.23 1.21 1.19 | 1.91 1.81 1.77 1.75 1.74 | 2.24 2.15 2.12 2.11 2.10 | 2.48 2.40 2.38 2.37 2.36 | 2.67 2.60 2.58 2.57 2.56 | 2.83 2.77 2.75 2.74 2.73 | 2.96 2.91 2.89 2.88 2.87 | 3.08 3.02 3.01 3.00 2.99 | 3.18 3.13 3.11 3.10 3.10 |
| 6 7 8 9 10 | 1.18 1.17 1.17 1.16 1.16 | 1.73 1.73 1.72 1.72 1.72 | 2.09 2.09 2.08 2.08 2.08 | 2.35 2.35 2.35 2.34 2.34 | 2.56 2.55 2.55 2.55 2.55 | 2.73 2.72 2.72 2.72 2.72 | 2.87 2.86 2.86 2.86 2.86 | 2.99 2.99 2.98 2.98 2.98 | 3.09 3.09 3.09 3.09 3.09 |
| ∞ | 1.13 | 1.69 | 2.06 | 2.33 | 2.53 | 2.70 | 2.85 | 2.97 | 3.08 |
摘自 Beyer WH: Handbook of Tables for Proba-bility and Statistics,second edition,p 386,CRC Press,Inc.,1979
式中A为系数,由表3查出。表3中n、k的意义同式(2)。
表3 由R作总体均数区间估计的系数A
上行: A0.05,下行: A0.01
| 组数 k | 每 组 例 数,n | ||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 6.36 31.9 | 1.30 3.00 | .719 1.36 | .505 .865 | .402 .673 | .336 .514 | .291 .430 | .256 .379 | .232 .338 |
| 2 | .879 2.11 | .316 .474 | .206 .312 | .154 .227 | .125 .179 | .106 .150 | .093 .131 | .084 .116 | .076 .105 |
| 3 | .360 .660 | .156 .273 | .104 .150 | .079 .112 | .065 .091 | .056 .077 | .049 .068 | .044 .060 | .040 .054 |
| 4 | .210 .350 | .096 .142 | .065 .092 | .050 .070 | .042 .057 | .036 .048 | .032 .043 | .028 .038 | .026 .035 |
| 5 | .140 .226 | .066 .095 | .046 .063 | .035 .049 | .030 .040 | .025 .034 | .022 .030 | .020 .027 | .018 .025 |
| 6 | .102 .157 | .050 .070 | .034 .047 | .027 .036 | .022 .030 | .019 .026 | .017 .023 | .015 .020 | .014 .019 |
| 7 | .079 .117 | .039 .055 | .027 .037 | .021 .029 | .018 .024 | .015 .020 | .013 .018 | .012 .016 | .011 .015 |
| 8 | .063 .094 | .032 .044 | .022 .030 | .017 .023 | .014 .019 | .012 .016 | .011 .014 | .010 .013 | .009 .012 |
| 9 | .053 .076 | .027 .036 | .018 .025 | .014 .019 | .012 .016 | .010 .014 | .009 .012 | .008 .011 | .007 .010 |
| 10 | .044 .064 | .023 .031 | .016 .021 | .012 .016 | .010 .014 | .009 .012 | .008 .010 | .007 .009 | .006 .008 |
摘自 Bauer EL: A Statistical Manual for Chemists,second edition,p 165,Academic Press,1971
例1 一份水样中氟化物的5次测定值 (mg/L)为0.48,0.37,0.47,0.40,0.43。试由其极差估计标准差。
R=0.48-0.37=0.11,n=5,k=1。查表2,c5,1=2.48,代入式(2)得
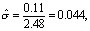
即标准差的估计值为0.044mg/L。
例2 测得32名从事某作业工人的血红蛋白量(g/dl),见表4。试由其极差估计标准差。
表4 32名某作业工人的血红蛋白量(g/dl)
| 变 量 值 | R | ||||||||
| 14.8 15.1 15.6 14.5 | 15.4 15.3 14.6 16.4 | 15.5 14.2 15.9 15.2 | 13.7 14.8 15.5 12.5 | 14.4 14.9 14.7 14.4 | 14.1 14.3 14.4 17.0 | 14.4 12.8 13.8 15.2 | 14.4 13.4 15.4 14.4 | 1.8 2.5 2.1 4.5 | |
| R | 1.1 | 1.8 | 1.7 | 3.0 | 0.5 | 2.9 | 2.4 | 2.0 | |
随机将32个变量值分成8组,如表4各纵列,并将各组极差列于表4末行,算得
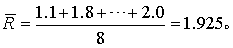
n=4,k=8,查表2,得c4,8=2.08,按式(2):
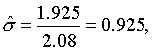
如按横行分组,并将各组极差列于表4的右侧,同理算得=2.725, n=8, k=4。 查表2, c84 -2.88,则
 =2.725/2.88=0.946g/dl,与上述结果很接近。
=2.725/2.88=0.946g/dl,与上述结果很接近。例3 表4资料的均数=14.72g/dl,求总体均数的95%可信区间。
按纵列分组,得∑R =15.4,n=4,k=8。查表3,A0.05=0.022,按式(3)得
(14.72-0.022×15.4,14.72+0.022×15.4)=(14.38,15.06),
即该作业工人的平均血红蛋白量的95%可信区间为14.38~15.06g/dl。
如按横行分组,同理得95%可信区间为14.37~15.07g/dl,与上述结果很接近。
容许区间估计 对总体中个体值分布范围的估计称容许区间估计,如95%容许区间表示总体中95%的个体值在此范围内,而在此范围以外,两侧尾部各有2.5%的个体值。容许区间常简写为TI。计算公式为
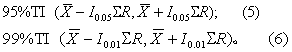
式中I为系数,由表5查出。n、k的意义同式(2)。例4 用表4资料估计总体中个体值的95%容许区间。按纵列分组得:∑R=15.4,n=4,k=8。查表5,I0.05 = 0.124。由例3, = 14.72。 按式(5):
(14.72-0.124×15.4,14.72+0.124×15.4)=(12.81,16.63),
即某作业工人中约有95%的人血红蛋白量在12.81~16.63g/dl范围内。
如按横行分组时,得95%TI为12.75~16.69g/dl,与上述结果很接近。
表5 由R作容许区间估计的系数I
上行: I0.05,下行: I0.01
| 组数 k | 每 组 例 数,n | ||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 8.99 45.1 | 2.25 5.20 | 1.44 2.72 | 1.13 1.93 | .985 1.65 | .889 1.36 | .823 1.22 | .768 1.14 | .734 1.07 |
| 2 | 1.76 4.22 | .774 1.16 | .583 .882 | .487 .718 | .433 .620 | .397 .561 | .372 .524 | .356 .492 | .340 .470 |
| 3 | .882 1.62 | .486 .819 | .360 .520 | .306 .434 | .276 .386 | .257 .353 | .240 .333 | .229 .312 | .219 .296 |
| 4 | .594 .990 | .332 .492 | .260 .368 | .224 .313 | .206 .279 | .190 .254 | .181 .243 | .168 .228 | .164 .221 |
| 5 | .443 .715 | .256 .368 | .206 .282 | .175 .245 | .164 .219 | 148 .201 | .139 .190 | .134 .181 | .127 .177 |
| 6 | .353 .544 | .212 .297 | .166 .230 | .148 .197 | .132 .180 | .123 .168 | .118 .159 | .110 .147 | .108 .145 |
| 7 | .296 .438 | .179 .252 | .143 .196 | .124 .172 | 117 .156 | .105 .140 | .097 .135 | .095 .127 | .092 .124 |
| 8 | .252 .376 | .157 .216 | .124 .170 | .108 .145 | .097 .132 | .090 .120 | .088 .112 | .085 .110 | .080 .108 |
| 9 | .225 .322 | .140 187 | .108 .150 | .094 .127 | 088 .118 | .079 .111 | .076 .101 | .072 .099 | .066 .095 |
| 10 | .197 .286 | .126 .170 | .101 .133 | .085 .113 | .077 .108 | .075 .100 | .072 .089 | .066 .085 | .060 .080 |
摘自 Bauer EL: A Statistical Manual for Chemists,second edition,p 166,Academic Press,1971
假设检验
样本均数与总体均数的比较 用L检验。按式(7)计算统计量L值。
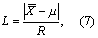
表6 极差分析用L界值表
| n | P(1):0.05 P(2):0.10 | 0.025 0.05 | 0.01 0.02 | 0.005 0.01 |
| 2 3 4 5 | 3.175 0.885 0.529 0.388 | 6.353 1.304 0.717 0.507 | 15.910 2.111 1.023 0.685 | 31.828 3.008 1.316 0.843 |
| 6 7 8 9 10 | 0.312 0.263 0.230 0.205 0.186 | 0.399 0.333 0.288 0.255 0.230 | 0.523 0.429 0.366 0.322 0.288 | 0.628 0.507 0.429 0.374 0.333 |
摘自 Beyer WH: Handbook of Tables for Probabi-lity and Statistics,second edition,p 380,CRCPress,Inc.,1979
配对计量资料的比较 用L检验。按式(8)计算统计量L值。
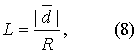
 为配对计量数据差值d的均数, R为d的极差。算得L值后,查表6L界值表得P值,按所取检验水准作出推断结论。
为配对计量数据差值d的均数, R为d的极差。算得L值后,查表6L界值表得P值,按所取检验水准作出推断结论。两样本均数的比较 用M检验。按式(9)计算统计量M值。
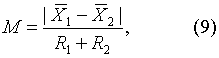
表7 极差分析用M界值表
| n1 | n2 | P(1):0.05 P(2):0.10 | 0.025 0.05 | 0.01 0.02 | 0.005 0.01 | n1 | n2 | P(1):0.05 P(2):0.10 | 0.025 0.05 | 0.01 0.02 | 0.005 0.01 |
| 4 | 4 5 6 7 8 9 10 15 20 | .322 .282 .256 .237 .224 .213 .204 .178 .164 | .407 .353 .319 .294 .276 .263 .252 .218 .200 | .526 .450 .403 .370 .346 .327 .313 .268 .246 | .620 .528 .469 .429 .399 .377 .359 .306 .279 | 9 | 9 10 15 20 | .137 .131 .112 .102 | .167 .160 .136 .124 | .205 .195 .165 .150 | .233 .221 .187 .169 |
| 10 | 10 12 14 16 18 20 | .125 .116 .109 .104 .100 .097 | .152 .141 .133 .126 .121 .117 | .186 .171 .161 .153 .147 .142 | .210 .194 .182 .173 .165 .160 | ||||||
| 5 | 5 6 7 8 9 10 15 20 | .247 .224 .208 .195 .186 .178 .155 .142 | .307 .277 .256 .240 .228 .218 .189 .173 | .387 .347 .319 .299 .282 .270 .232 .212 | .450 .402 .368 .343 .323 .309 .263 .240 | ||||||
| 12 | 12 14 16 18 20 | .107 .101 .096 .092 .089 | .130 .122 .116 .111 .107 | .158 .148 .140 .134 .130 | .178 .167 .158 .151 .146 | ||||||
| 14 | 14 16 18 20 | .094 .090 .086 .083 | .114 .108 .104 .101 | .138 .131 .125 .121 | .156 .147 .141 .135 | ||||||
| 6 | 6 7 8 9 10 15 20 | .203 .188 .177 .168 .161 .139 .128 | .250 .240 .217 .206 .197 .169 .155 | .312 .287 .268 .254 .242 .207 .189 | .329 .329 .307 .289 .276 .235 .214 | ||||||
| 16 | 16 18 20 | .085 .081 .078 | .103 .098 .094 | .124 .118 .114 | .139 .133 .128 | ||||||
| 18 | 18 20 | .077 .074 | .093 .090 | .113 .108 | .126 .121 | ||||||
| 7 | 7 8 9 10 15 20 | .174 .163 .155 .148 .128 .117 | .213 .200 .189 .181 .155 .142 | .263 .246 .233 .222 .189 .172 | .301 .281 .265 .252 .214 .195 | ||||||
| 20 | 20 | .071 | .086 | .104 | .116 | ||||||
| 8 | 8 9 10 15 20 | .153 .145 .139 .119 .109 | .187 .177 .169 .144 .132 | .231 .217 .207 .176 .160 | .262 .247 .235 .199 .180 |
摘自 Moore PG: The two-sample t-test based on range,Biometrika,44: 487,1957
例5 从加锰30.0μg/L的自来水中取5份水样测锰(μg/L),得28.9、29.0、30.0、29.1、28.5,算得均数=29.1。 问本法测得均数是否低于加入量。
H0: μ=30.0,H1: μ<30.0。单侧α=0.05。
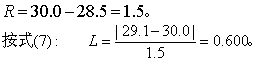
查表6,n=5,得0.025>P>0.01,按α=0.05水准拒绝H0,接受H1,可认为本法测得的锰量低于加入量。
例6 10名受试者的尿样分别经4.5小时与28小时消化时间的尿汞测定值见表8,问不同消化时间的测定值有无差别?
H0: μ=0,H1: μ≠0。α=0.05。
表8 不同消化时间尿汞测定值(mg/L)
| 编号 | 消化时间(小时) | 差值 d | |
| 4.5 | 28 | ||
| 1 2 3 4 5 6 7 8 9 10 | 0.040 0.227 0.109 0.077 0.098 0.092 0.195 0.079 0.075 0.033 | 0.055 0.267 0.086 0.109 0.118 0.103 0.210 0.091 0.109 0.043 | -0.015 -0.040 0.023 -0.032 -0.020 -0.011 -0.015 -0.012 -0.034 -0.010 |
| -0.166 | |||
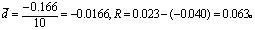
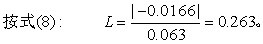
查表6,n=10,得0.05>P>0.02,按a=0.05水准拒绝H0,接受H1,故可认为两种消化时间的尿汞测定结果不同,消化时间为28小时者尿汞测定值较高。
例7 表9中为两组人尿中17酮类固醇的排出量,试比较两组均数有无差别。
表9 老年性慢性支气管炎病人与健康人
尿中17酮类固醇排出量(mg/24h)
| 健康人组 | 病人组 |
| 8.79 3.14 6.46 3.72 6.64 4.01 5.60 4.57 7.71 4.99 | 2.90 5.41 5.48 4.60 4.03 5.10 5.92 4.97 4.24 4.36 2.72 2.37 2.09 7.10 |
| 55.63 | 61.29 |
H0: μ1 =μ2,H1: μ1≠μ2。
a=0.05。
健康人组 n1= 10,1,=55.63/10=5.56,
R1=8.79-3.14=5.65;
病人组 n2=14,2,=61.29/14=4.38,
R2=7.10-2.09=5.01。
按式(9):
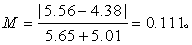
☚ 序列的随机性检验 协方差分析 ☛
- 广告伦理纲要是什么意思
- 广告位置是什么意思
- 广告体是什么意思
- 广告促销是什么意思
- 广告信任度是什么意思
- 广告信息策略是什么意思
- 广告公司是什么意思
- 广告公司经理是什么意思
- 广告公司(广告社)是什么意思
- 广告决定性瞬间是什么意思
- 广告决策是什么意思
- 广告出版物是什么意思
- 广告刊户是什么意思
- 广告刊播价格是什么意思
- 广告列车是什么意思
- 广告创作“五i”要素是什么意思
- 广告创作基本原则是什么意思
- 广告创作法规是什么意思
- 广告创作的文体是什么意思
- 广告创意是什么意思
- 广告制作公司是什么意思
- 广告制作单位是什么意思
- 广告刺激强化律是什么意思
- 广告功能是什么意思
- 广告协会是什么意思
- 广告印刷品是什么意思
- 广告及招揽顾客的禁止是什么意思
- 广告发布/商务合作是什么意思
- 广告发布者是什么意思
- 广告口号是什么意思
- 广告合同是什么意思
- 广告名片是什么意思
- 广告员是什么意思
- 广告品是什么意思
- 广告商是什么意思
- 广告商标是什么意思
- 广告回信是什么意思
- 广告回单是什么意思
- 广告团体组织是什么意思
- 广告图样是什么意思
- 广告图画是什么意思
- 广告夹是什么意思
- 广告女郎是什么意思
- 广告如何利用报纸是什么意思
- 广告婚礼是什么意思
- 广告媒介是什么意思
- 广告媒介物是什么意思
- 广告媒介目标是什么意思
- 广告媒介组合策略是什么意思
- 广告媒体是什么意思
- 广告媒体研究是什么意思
- 广告媒体选择的心理因素是什么意思
- 广告学是什么意思
- 广告学会是什么意思
- 广告定位是什么意思
- 广告实施原则是什么意思
- 广告审查是什么意思
- 广告客户是什么意思
- 广告宣传心理是什么意思
- 广告宣传活动是什么意思