双曲线的性质
双曲线的性质shuangquxian de xingzhi
❶对称性双曲线是轴对称图形,有两条互相垂直的对称轴,一条与双曲线有交点,一条与双曲线没有交点.它也是中心对称图形,对称中心就是两对称轴的交点,叫做双曲线的中心.双曲线和对称轴的交点叫做双曲线的顶点,连结两顶点的线段叫做双曲线的实轴.
双曲线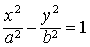 的对称轴是两坐标轴,中心是原点,两顶点是A′(-a,0)和A (a,0),实轴|AA′|=2a,连结B′(0,-b)和B(0,b)的线段B′B叫做双曲线的虚轴,|B′B|=2b(如图1).
的对称轴是两坐标轴,中心是原点,两顶点是A′(-a,0)和A (a,0),实轴|AA′|=2a,连结B′(0,-b)和B(0,b)的线段B′B叫做双曲线的虚轴,|B′B|=2b(如图1).
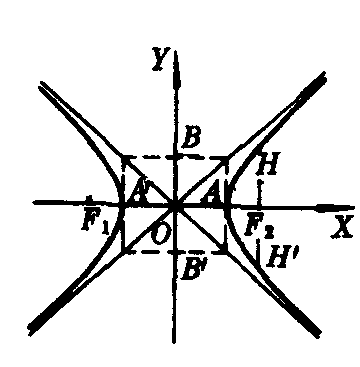
图1
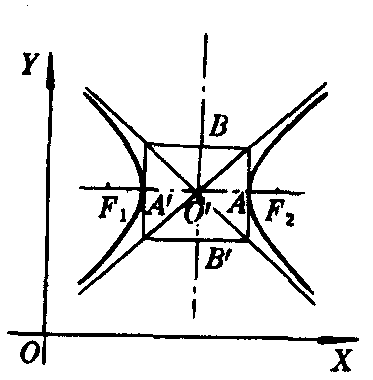
图2
| 双曲线 |
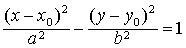
| 的对称轴是直线x |
❷渐近性 双曲线有两条渐近线,渐近线相交于双曲线的中心,双曲线的两条对称轴平分两渐近线的
| 夹角. 双曲线 |
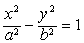
| 的两条渐近线是 |
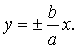
| 这两条渐近线方程常写成 |
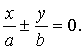
❸区域性 双曲线是无限伸展的,但是位于过顶点垂直于实轴的两直线和两条渐近线围成的平面区域内.
| 综上所述,双曲线 |
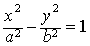
| 位于直线x=±a和 |
| 渐近线 |
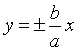
| 所围成的平面区域内. 由于直线y= |
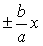
| 重合于由 |
| x=±a, y=±b |
| 四条直线所组成的矩 |
❹ 形状可变性 由于 |
| c>a>0, |
| 离心率 |
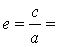
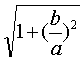
| 恒大于1,e越接近于1, |
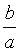
| 越接近于零, |
| 双曲线 |
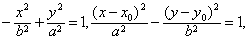
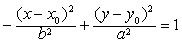
| 也有类似的性质. |
☚ 双曲线的标准方程 双曲线的焦点 ☛
- 二、邮电通讯设施建设是什么意思
- 二、邯郸、邢台旅游区是什么意思
- 二、郊区城镇体系布局是什么意思
- 二、酒泉子·每见惶惶是什么意思
- 二、采用国际标准和企业标准化是什么意思
- 二、释语是什么意思
- 二、重大国际农业会议是什么意思
- 二、重构农村商品流通的“主渠道”是什么意思
- 二、金文是什么意思
- 二、金笛是什么意思
- 二、金蛇郎君小曲是什么意思
- 二、金融体系是什么意思
- 二、金融市场功能是什么意思
- 二、金融统计作用是什么意思
- 二、铁路运输是什么意思
- 二、银南旅游区是什么意思
- 二、镇江旅游区是什么意思
- 二、长江干流及主要支流防洪是什么意思
- 二、问候有关亲友是什么意思
- 二、间接析数是什么意思
- 二、间隔异称是什么意思
- 二、降雨是什么意思
- 二、陕甘宁边区时期的陇东民主政权建设是什么意思
- 二、陕西省农业厅是什么意思
- 二、陕西省农业厅所属县级以上企事业单位是什么意思
- 二、隋唐五代是什么意思
- 二、隋唐五代两宋是什么意思
- 二、集体经济和农户的农业投入是什么意思
- 二、集团化农业科技承包是什么意思
- 二、集市贸易的作用是什么意思
- 二、集贸市场发展与建设是什么意思
- 二、集贸市场建设是什么意思
- 二、集贸市场的作用是什么意思
- 二、集贸市场的发展与建设是什么意思
- 二、集镇建设成就是什么意思
- 二、集镇建设的成就和经验是什么意思
- 二、青岛市是什么意思
- 二、青年、民兵、妇女等群众组织是什么意思
- 二、青海省农业厅是什么意思
- 二、青海省农业厅直属企事业单位是什么意思
- 二、青海省农林学校是什么意思
- 二、青海省农林科学院是什么意思
- 二、非耕地资源开发利用的历史演变是什么意思
- 二、面向市场,调整农村产业结构是什么意思
- 二、革命根据地的基层政权是什么意思
- 二、预言示现是什么意思
- 二、风格即其人是什么意思
- 二、食油购销是什么意思
- 二、饲料加工工业是什么意思
- 二、饲料工业是什么意思
- 二、饲料工业建设是什么意思
- 二、饲料工业现状是什么意思
- 二、香港的货币政策工具及其操作主体是什么意思
- 二、骨干工程是什么意思
- 二、高、中等农业专业教育是什么意思
- 二、高中等林业院校是什么意思
- 二、高新技术在农业上的应用是什么意思
- 二、高等农业专业教育是什么意思
- 二、高等农业教育的发展历程是什么意思
- 二、高等院校是什么意思