既然微观粒子体系的状态要用波函数来描述,那么,如何能够得知某一体系,譬如绕氢原子核运动的电子的波函数呢?这一问题类似于宏观体系中,已知某一时刻质点的坐标和动量求任一时刻质点的坐标和动量,解决这一问题的基础是牛顿运动方程
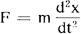
式中F是作用于质点上的力,m是质点的质量,x是质点的坐标,t是时间,这一方程不是由其它更基础的定理,定律通过数学演绎或逻辑推理的方法得来的,而是从实验中总结、概括出来的,其正确性要靠由此推出的结论是否与实验相一致来判断。
对于微观粒子,自然也应该有一个其作用类似于牛顿运动方程,用来描述体系随时间变化规律的方程。波函数ψ(q,t)随时间的变化规律要由薛定谔方程
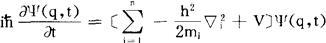
来描述。式中i是虚数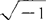 ,
,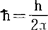 ,h是普朗克常数,t是时间,mi是第i个粒子的质量,v是体系的势能,
,h是普朗克常数,t是时间,mi是第i个粒子的质量,v是体系的势能,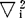 是表示下列运算的符号
是表示下列运算的符号
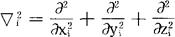
称为拉普拉斯算符。
对于单个粒子体系,上述薛定方程简化为
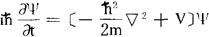
同牛顿方程一样,描述微观粒子基本运动规律的薛定谔方程也是客观规律,也不能根据其他定理、定律通过逻辑推理和数学演绎的方法得到,而只能从科学实验中概括出来,其正确性只能由实验来验证,只是不象牛顿方程那样直观。
实验证明薛定谔方程是正确的。
对于定态,可以证明定态波函数所满足的方程是
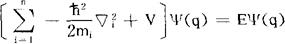
式中E是体系的能量,对于单粒子体系,上式简化为
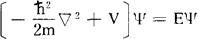
为区分起见,将ψ(q,t)满足的方程称为包含时间的薛定谔方程,而将定态波函数ψ(q)所满足的方程称为定态薛定谔方程
常将包含时间的薛定谔方程写成
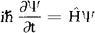
式中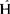 称为哈密顿算符,对于n个粒子体系,
称为哈密顿算符,对于n个粒子体系,
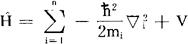
对于单粒子体系
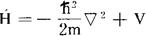
采用哈密顿算符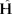 ,定态薛定谔方程可写为
,定态薛定谔方程可写为
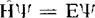
- 濹是什么意思
- 濺是什么意思
- 濺泉是什么意思
- 濻是什么意思
- 濼是什么意思
- 濼源橋是什么意思
- 濽是什么意思
- 濽淌是什么意思
- 濾是什么意思
- 濿是什么意思
- 瀀是什么意思
- 瀀渥是什么意思
- 瀁是什么意思
- 瀁瀁是什么意思
- 瀂是什么意思
- 瀃是什么意思
- 瀄是什么意思
- 瀄汨是什么意思
- 瀅是什么意思
- 瀆是什么意思
- 瀆山大玉海是什么意思
- 瀇是什么意思
- 瀇滉是什么意思
- 瀇瀁是什么意思
- 瀈是什么意思
- 瀉是什么意思
- 瀉土是什么意思
- 瀉白散是什么意思
- 瀉青丸是什么意思
- 瀉鹵是什么意思
- 瀉黄散是什么意思
- 瀊是什么意思
- 瀋是什么意思
- 瀋陽故宫是什么意思
- 瀌是什么意思
- 瀌瀌是什么意思
- 瀌雨是什么意思
- 瀍是什么意思
- 瀍桥是什么意思
- 瀍橋是什么意思
- 瀎是什么意思
- 瀎壁是什么意思
- 瀎布是什么意思
- 瀎泧是什么意思
- 瀎潏是什么意思
- 瀎灰是什么意思
- 瀏是什么意思
- 瀏溧是什么意思
- 瀏濫是什么意思
- 瀏瀏是什么意思
- 瀏蒞是什么意思
- 瀏陽石是什么意思
- 瀐是什么意思
- 瀑是什么意思
- 瀑垂天绅是什么意思
- 瀑声穿竹到深枕,雨气逼花香半湖。是什么意思
- 瀑布是什么意思
- 瀑布、溶洞、暗河、峡谷是什么意思
- 瀑布园是什么意思
- 瀑布垂直泻下是什么意思