指无偏估计量的方差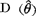 ,不可以任意小,在某些条件下(有关的概率密度或分布律关于参数可微,并且微分和积分次序可以交换),它的方差的下界由罗一克诺美(Rao-Cramer)不等式给出:
,不可以任意小,在某些条件下(有关的概率密度或分布律关于参数可微,并且微分和积分次序可以交换),它的方差的下界由罗一克诺美(Rao-Cramer)不等式给出:
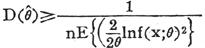
虽然这个下界依赖于总体的概率密度或分布律f(x;θ),也依赖于样本容量n,如果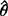 是参数θ的一个无偏估计量,它的方差达到上式给出的下界,则称
是参数θ的一个无偏估计量,它的方差达到上式给出的下界,则称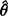 是有效估计量。
是有效估计量。
对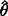 的任一无偏估计量
的任一无偏估计量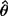 ,设它的方差为D(θ1),记:
,设它的方差为D(θ1),记:
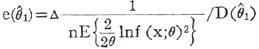
上式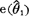 则称为无偏估计量
则称为无偏估计量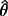 的有效率。满足前述条件的无偏估计量
的有效率。满足前述条件的无偏估计量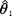 1,其有效率满足
1,其有效率满足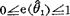 ,有效估计量
,有效估计量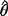 的有效率
的有效率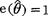 。
。
- 李滉是什么意思
- 李滉是什么意思
- 李滋煊是什么意思
- 李滔是什么意思
- 李满住是什么意思
- 李满天是什么意思
- 李满天是什么意思
- 李满红是什么意思
- 李满红是什么意思
- 李漪是什么意思
- 李潆是什么意思
- 李潜夫是什么意思
- 李潭德是什么意思
- 李潼是什么意思
- 李潼关是什么意思
- 李澂是什么意思
- 李澂是什么意思
- 李澄之是什么意思
- 李澄宇是什么意思
- 李澍恩是什么意思
- 李澍田是什么意思
- 李澣是什么意思
- 李澥是什么意思
- 李濂是什么意思
- 李濂是什么意思
- 李濂是什么意思
- 李濂是什么意思
- 李濂镗是什么意思
- 李瀚章是什么意思
- 李瀚章是什么意思
- 李瀚章是什么意思
- 李瀷是什么意思
- 李瀷是什么意思
- 李瀷是什么意思
- 李瀷是什么意思
- 李灏是什么意思
- 李火凤是什么意思
- 李灼成是什么意思
- 李灿是什么意思
- 李灿是什么意思
- 李灿是什么意思
- 李灿是什么意思
- 李灿是什么意思
- 李灿是什么意思
- 李炎是什么意思
- 李炎是什么意思
- 李炎光是什么意思
- 李炎秋是什么意思
- 李炜如是什么意思
- 李炭是什么意思
- 李炯基是什么意思
- 李炯才是什么意思
- 李炯涛是什么意思
- 李炳是什么意思
- 李炳之是什么意思
- 李炳凯是什么意思
- 李炳勋是什么意思
- 李炳南是什么意思
- 李炳夫是什么意思
- 李炳寰是什么意思