微扰法

---

解薛定谔方程的一种近似方法。

对于薛定谔方程

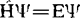(1)

若不能精确求解，但若其中哈密顿算符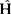可写成两部分之和

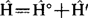
而方程

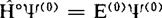(2)

能够精确求解，而且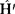′只占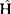中的很小一部分，就好像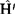′是对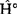的一个微小的扰动。这时就可把方程(1)的解看成是由两部分组成，其主要部分是方程(2)的解ψ⁽⁰⁾和E⁽⁰⁾，这称为零级近似波函数和零级近似能量，其次要部分是由于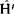的存在而对φ⁽⁰⁾和E⁽⁰⁾的修正φ⁽¹⁾和E⁽¹⁾，分别称为一级波函修正和一级能量修正，而方程(1)的近似解可以写作

φ⁽⁰⁾+φ⁽¹⁾

和

E⁽⁰⁾+E⁽¹⁾

分别称为一级近似波函数和一级近似能量。

ψ⁽¹⁾和E⁽¹⁾可以通过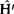′、φ⁽⁰⁾和E⁽⁰⁾而计算。

随著对其精确度要求的增加，还可继而计算其二级、三级波函数修正和能量修正φ⁽²⁾，…φ⁽³⁾E⁽²⁾，E⁽³⁾…，从而可得其精确度更高的二级、三级等近似波函数和近似能量。

φ⁽⁰⁾+φ⁽¹⁾+φ(2)+…

E⁽⁰⁾+E⁽¹⁾+E⁽²⁾+…