地理系统的线性规划方法

---

线性规划是运筹学中规划理论的分支之一，其主要研究带线性等式或不等式约束的线性函数的极小化或极大化问题。

线性规划模型的基本结构要素包括：变量、约束条件和目标函数。变量(或称决策变量)是决策者对问题需要考虑和控制的因素，一般以X₁₁，X₁₂，……，X_ij表示。

约束条件是实现目标的资源限制条件，它是含有决策变量的线性表达式。目标函数是决策者在对问题明确之后所要达到的经济目的。如产量最高、利润最大、效率最高、成本最低、费用最少、时间最短等等。其数学表达式为线性函数的极值问题，并含有代表解决问题的决策变量及其对目标的各种影响。总之，线性规划是求一组变量的值，在满足一定的约束条件下，求得目标函数最优解问题。

其数学模型为：

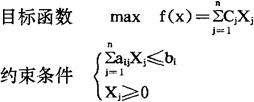
这种方法被广泛地应用于军事、工业、农业、城市规划、经济等各个领域。

60年代由于电子计算机的产生和发展，使这一方法如虎添翼，在各个领域中发挥著越来越大的作用。