回归分析

---

Y=a+bX

所示，X变动一个单位，则Y必然变动b个单位，这种关系就是确定性关系，亦称为线性函数关系。

对于回归关系，以上面的Y和X为例，可以用如下的线性等式描述。

Y=a+bX+u

这里的u是一个随机变量，服从正态分布，均值为零，方差存在且有限。这里的回归方程反映的是不确定性关系，可以描述为X变动一个单位，Y平均变动b个单位，回归分析的结论是“可能”的，或者一般性的，不绝对，不肯定。对于上式，可以给出回归分析的基本思想：

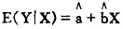
即Y在X给定时的条件期望为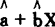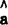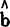，、是a、b的估计值。

对于多元线性回归关系，有被解释变量向量Y和解释变量X，它们的观测值有n个，有下面用矩阵表达的回归方程式：

Y=XB+u

式中，X是解释变量矩阵，n行，p+1列；B是待估回归系数向量，已估参数用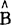表示；u是随机扰动项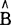；=[X’X]^－1X’Y。

线性回归有以下几个重要假设：
❶ Y服从多元正态分布；
❷ E(Y)=XB；
❸ cov(Y)=cov(Y)=σ²I。