极值jizhi

设函数y=f(x)在点x₀的邻域内有定义，若存在x₀的某邻域(x₀-δ,x₀+δ)，在此邻域内恒有f(x₀)≥f(x)(f(x0)≤f(x))则称f(x₀)为f(x)的一个极大值（极小值），点x0称为极大值点（极小值点）.极大值与极小值统称为极值，极大值点与极小值点统称为极值点.

图1

例如，函数f(x)=x³-6x²+9x+16，在(-∞,1)内是单调增的，在(1,3)内是单调减的，在(3,+∞)内又是单调增的.而在邻域(1-δ,1+δ)，恒有f(x)≤f(1)；在邻域(3-δ,3+δ)，恒有f(x)≥f(3).所以f(1)=20为f(x)的极大值，点1为极大值点；而f(3)=16为f(x)的极小值，点3为极小值点.从f(x)=x³-6x²+9x+16的图象上，可以直观地看到它在(-∞,1)内上升，在(1,3)内下降，在(3,+∞)内上升，而点(1,20)是曲线上一个高峰，点(3,16)是曲线上一个低谷(如图1).实际上它们分别反映出函数的极大值和极小值.
函数的极值只是在一点的邻域这样一个很小范围内的最大值和最小值，所以它是局部性的.一个定义在区间〔a.b〕上的函数可以有许多个极大值和极小值，并且其中极大值不一定都大于每一个极小值(如图2).

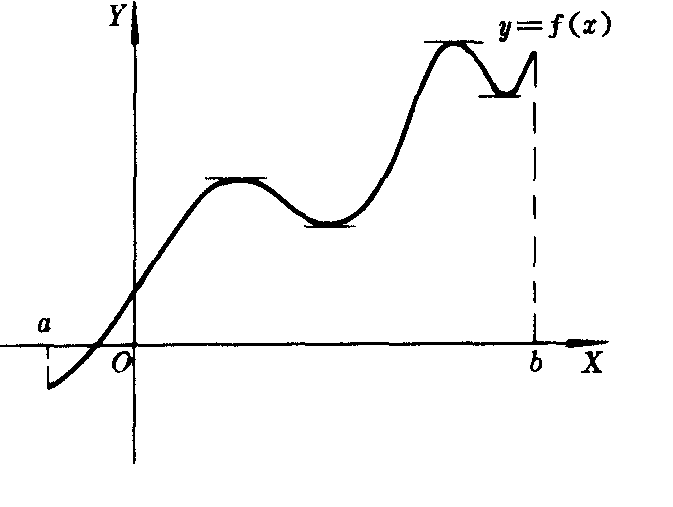
图2

确定一个函数的极值，可以有很多方法.最基本的方法是从判断函数的增减性中求得函数的极值.特殊地，对二次函数可以用配方法；对某些函数可以利用平均值不等式；对某些有理函数可以用判别式法.更一般的方法是利用微积分的有关知识求出函数的极值.

极值

函数的极大值和极小值的总称。若函数y=f(x)在点x₁处的函数值f(x₁)都比x₁附近的其他点的函数值大（小），称为f(x)在x₁取到极大（小）值。如y=sinx在-π/2处取极小值-1，在π_/2处取极大值1。

极值Extremum

函数在其定义域的某些局部区域所达到的相对最大值或相对最小值。当函数在其定义域的某一点的值大于该点周围任何点的值时，称函数在该点有极大值； 当函数在其定义域的某一点的值小于该点周围任何点的值时，称函数在该点有极小值。这里的极大和极小只具有局部意义。因为函数的一个极值只是它在某一点附近的小范围内的极大值或极小值。函数在其整个定义域内可能有许多极大值或极小值，而且某个极大值不一定大于某个极小值。函数的极值通过其一阶和二阶导数来确定。对于一元可微函数f (x)，它在某点x₀有极值的充分必要条件是一阶导数f(x₀₎等于零而二阶导数f″ (x₀₎ 连续；在f′(x₀₎ =0而f″(x₀₎ >0时，f(x₀₎ 为一极大值。对于多元可微函数。

y=f (x₁,x₂，…，x_n)

它在点 (x₁,x₂，…，x_n)处有极小值的充分必要条件是所有一阶偏导数零而所有二阶偏导数组成的矩阵的n个主子式为正。以f_i表示一阶偏导数∂f/∂x_i,i=1, 2，…，n)，以f_ij表示二阶偏导数

,(i,j=1,2，…，n),
则此充分必要条件就是：

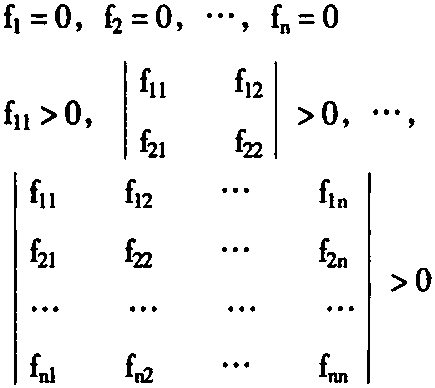
函数y=f(x₁,x₂，…，x_n)在点(x₁,x₂，…，x_n)有极大值的必要条件是所有一阶偏导数等于零而所有二阶偏导数构成的矩阵的n个主子式的符号是负正交错出现。即：

函数极值在经济研究中应用很广。因为合理经济行为总是力求某种目标达于极大值或极小值。

极值

extreme;extremum