数学期望

简称“期望”。定义为：设ξ为随机变量，其分布函数为F(x),
若

存在，则记

称E(ξ)为ξ的数学期望。本定义所用积分为黎曼—斯蒂尔吉斯(R-S)积分。常被应用于测验分数统计中。

数学期望shuxue qiwang

设离散型随机变量的概率密度为P {X=x_k}=p_k,k=1,2,3，…，若级数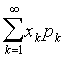绝对收敛，则称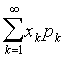为x的数学期望，简称期望或均值，记作E (X)，即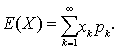
设连续型随机变量X的概率密度函数为f(x)，若积分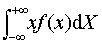绝对收敛，则称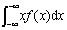为x的数学期望，简称期望或均值，记作E (X)，即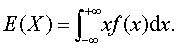
随机变量的数学期望具有以下性质：
❶E (C) =C,C是常数；

❷E (X+Y) =E (X) +E (Y);

❸E (kX) =kE (X),k是常数；

❹设X,Y是相互独立随机变量，且E(x),E (Y)存在，则E (XY) =E (X) ·E (Y)。
应当注意，当说数学期望表示随机变量的平均值时，是指随机变量独立地取比较多的值，这些值的平均值稳定在随机变量的数学期望上。其次，数学期望表示随机变量的平均位置特征。
特别指出的是，并不是所有随机变量都有它的数学期望值，如服从柯西分布的随机变量X就不存在数学期望，它的概率密度函数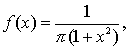-∞ dx不收敛。

数学期望

又称“均值”。随机变量重要的数字特征。反映随机变量的平均取值。通常随机变量ζ的数学期望记为Eζ或Mζ。如果一随机变量ζ取值x₁,x₂，…，x_n的概率分别为p₁,p₂，…，p_n，则Eζ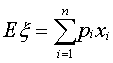。对于一般的随机变量，数学期望可由级数或积分表示。

数学期望mathematical expectation

是随机变量取值的平均。如总体平均数μ为随机变量X的数学期望，符号为E (x)。总体方差σ²为随机变量(x-μ)²的数学期望，符号为E〔(x-μ)²〕。μ和σ²是最主要的两个数学期望。各种分布的统计量均有它的数学期望。

数学期望mathematical expectation

亦称“期望”、“均值”。随机变量最基本数学特征之一。反映随机变量平均取值的大小，是简单算术平均的一种推广，类似加权平均。