数列的规律Shulie de guilu

数列中的数称为项， 排在第一位(或编号为1)的叫第1项，排在第n位(或编号为n)的叫第n项，也叫通项或一般项。数列的规律表现在相邻项之间的关项或者是项和它的编号的关系上。
例1: 总结以下数列的规律：
(a) 1, 2, 3, 4, 5, ……(b) 1, 4, 7, 10, 13, ……(c) 81, 77, 73, 69, 65, ……
(a)的每一项比前一项大1, (b)中数列的每一项比前一项大3, (c)中数列的每一项比前一项小4。这样的数列叫等差数列， 各项与前一项的差称为公差，(a) 中公差为1, (b) 中公差为3, (c) 中公差为-4。等差数列的一般形式为
a, a+d, a+2d, a+3d, a+4d, ……
它的一般项是a_n＝a+(n-1)d，这一公式叫等差数列的通项公式， 通项公式体现了项和编号之间的关系。
例2: 总结以下各数列的规律：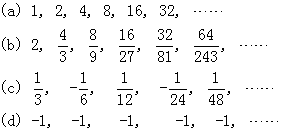
这些数列有一个共同的特点： 后项与前项的比为一固定的值， 在 (a) 中这一比值为2, 在(b)、(c)、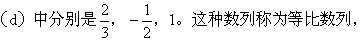
而后项与前项的固定比值称为公比， 等比数列的一般形式为a₁, a₁q, a₁q², a₁q³, a₁q⁴ ，……， 其中q为公比，a₁叫首项，其通项为a1q^n-1。此例(d)中的数列所有各项都相等，它既是等比数列又是等差数列。这样的数列叫做常数列。
例3: 求以下数列的通项：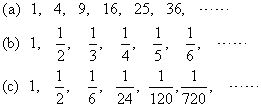
解： (a)数列可改写成1², 2², 3², 4², ……其通
例4:十三世纪初，意大利数学家伦纳德提出下面的有趣问题：兔子出生后，若每次不多不少恰好生一对（一雌一雄），假如养了初生的小兔一对，试问一年后共可有多少对兔子 （如果生下的小兔都不死的话）?
据题设， 可进行以下的推算：
第一个月， 有一对小兔。
第二个月， 仍为一对 （因小免尚不能生育）
第三个月， 有二对小兔 （小兔开始生育）
第四个月，有三对小兔(两个月前出生的小兔照常生育， 上个月出生的小兔尚不能生育)。
同样道理，第五个月将有五对小兔，第六个月将有八对小兔，第七个月将有十三对小兔，等等，于是得到下面的数列：
1, 1, 2, 3, 5, 8, 13, 21, ……
它的第n项代表第n个月小兔的对数， 相邻项之间的关系可以表示成a_n＝an-₁+a_n-₂(n≥3)这样的关系叫递推关系， 就是说各项的值可以通过一种统一的办法由它前面若干项计算出来， 上述数列叫做斐波那契数列，它虽然出自一个趣题，但是在优选法，几何图形的黄金分割、生物数学及计算理论等诸多纯粹数学和应用数学领域都找到了应用。
例5（第一届华罗庚金杯赛决赛第二试）:70个数排成一行，除了两头的两个数以外，每个数的3倍都恰好等于它两边两个数的和。这一行最左边的几个数是这样的：0, 1, 3,8,21, ……问最右边的一个数被6除余几？
解： 由题设， 可得下面的递推关系
a_n＝3an-₁-a_n-₂ (n≥3)。
从而，a_n-₂+a_n能被3整除，a₁＝0,a₃＝3都能被3整除， 因此a₁、a₃、a₅、a₇、a₉, ……都能被3整除。a₂＝1被3除余1, a₄被3除余2, 因此a₂,a₆,a₁₀, ……a2+4k, ……被3除余1,a70=a2+4x17被3除余1。又若a_n-₁,an-₂都是奇数， 则a_n＝3an-1-a_n-₂是偶数，若an_-1与a_n-₂为一奇一偶，则a_n＝3a_n-₁-an-₂为奇数，而a₁＝0为偶数，a₂＝1,a₃＝3为奇数，故a₁,a₄,a₇,a10……都是偶数，因此a₇₀是偶数。综上述a₇₀被3除余1，而且是偶数， 故a70被6除余4。