总体回归直线的估计
总体回归直线的估计
样本直线回归方程中,回归系数b和截距a是总体回归系数β和截距a*(注意勿与检验水准a相混)的估计值。即使实验条件不变,b与a也会有抽样波动。同理,样本回归值 Ŷ 及变量值Y亦有抽样波动。 为了说明回归方程的稳定性,就须对β、 a*和μŶ(总体回归值)、Y作出区间估计,也就是对总体回归直线作出区间估计。β及a*的区间估计 方法步骤如下:
(1) 计算样本直线回归方程,并作假设检验 (见条目“直线回归”)。若认为存在直线关系,则作区间估计,否则不必进行。
(2) 分别按式(1) 及式(2) 计算回归系数b的标准误sb及截距a的标准误sa。
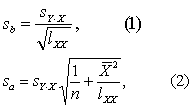
(3)查t界值表得ta(n-2)值,分别按式(3)及式(4)计算可信度为1-a时,β及a*的可信区间:
β为 (b-ta(n-2)sb,b+ta(n-2)sb),(3)
a*为 (a-ta(n-2)sa,a+ta(n-2)sa)。(4)可信度相同时,sb与sa愈小,β与a*的可信区间就愈小,回归方程就稳定。在实际使用回归方程时,愈稳定愈好。
μŶ及Y的区间估计 方法步骤如下:
(1) 同β及a*的区间估计步骤(1)。
(2)按观察值X的范围,选定若干Xi值,列出计算表(如下表)。 将Xi代入回归方程求得的回归值Ŷi是与Xi相应的个体值Yi的均数,而Yi值分布在均数Yi的上下,Ŷi的标准误sŶi(简记为sŶ)按式(5)计算,
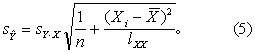
 (未知时,以Ŷi作为估计值)为均数,σYi [未知时,以sYi (简记为sY)作为估计值]为标准差的正态分布。sY按式(6)计算,
(未知时,以Ŷi作为估计值)为均数,σYi [未知时,以sYi (简记为sY)作为估计值]为标准差的正态分布。sY按式(6)计算,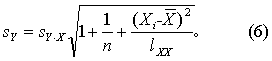
(3)查t界值表得ta(n-2)值,分别按式(7)计算可信度为1-a时,μŶ的可信区间;按式(8)计算Y的1-a容许区间。
μŶ的可信区间为 (Ŷ-ta(n-2)sŶ, Ŷ+ta(n-2)sŶ), (7)Y的容许区间为 (Ŷ-ta(n-2)sY, Ŷ+ta(n-2)sY)。 (8)式(8)算出的容许区间,医学上常用作给定X值时,相应Y值的正常值范围。 若n相当大,xi离较近时,则此范围近似的为
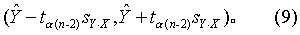
(4)绘回归直线, 并将上述求得的各X值对应的μŶ、Y区间的上限值、下限值画四条曲线 (注意不是直线),如图。 离回归直线近的两条曲线间是 μŶ的1-a可信区间,即总体回归直线的可能范围; 两条虚线间是各X值相应的Y值的1-a容许区间。理论上有5%的点子在两条虚线以外和正好落在线上。
例 某地18~25岁女青年50人的体重与体表面积资料(见图)的初步计算结果如下:
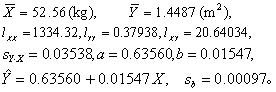
经直线回归方程的假设检验,体重与体表面积之间存在直线关系。试估计总体回归系数β与总体回归值μŶ的95%可信区间,以及个体值Y的95%容许区间。
求β的95%可信区间。今a=0.05,n=50,v=50-2=48,查t界值表,t0.05(50-2) = 2.011,由式(3)得
(0.01547-2.011×0.00097,0.01547+2.011×0.00097)=(0.0135,0.0174)。
故β的95%可信区间为0.0135~0.0174m2/kg。
求μŶ的95%可信区间与Y的95%容许区间。 选定Xi值,计算如表。
μŶ的可信区间及Y的容许区间的计算
| Xi (1) | Xi- (2) | Ŷi (3) | SŶi (4) | Ŷi±t0.05(48)SŶi | SYi (7) | Ŷi±t0.05(45)SYi | ||
| 下 限 (5) | 上 限 (6) | 下 限 (8) | 上 限 (9) | |||||
| 40 42 44 ⋮ | -12.56 -10.56 -8.56 ⋮ | 1.2544 1.2854 1.3163 ⋮ | 0.0132 0.0114 0.0097 ⋮ | 1.2279 1.2625 1.2968 ⋮ | 1.2809 1.3083 1.3358 ⋮ | 0.0377 0.0372 0.0367 ⋮ | 1.1786 1.2106 1.2425 ⋮ | 1.3302 1.3602 1.3901 ⋮ |
| 52 ⋮ | -0.56 ⋮ | 1.4400 ⋮ | 0.0050 ⋮ | 1.4299 ⋮ | 1.4501 ⋮ | 0.0357 ⋮ | 1.3682 ⋮ | 1.5118 ⋮ |
| 60 62 64 | 7.44 9.44 11.44 | 1.5638 1.5947 1.6257 | 0.0088 0.0104 0.0122 | 1.5461 1.5738 1.6012 | 1.5815 1.6156 1.6502 | 0.0365 0.0369 0.0374 | 1.4904 1.5205 1.5505 | 1.6372 1.6689 1.7009 |
Xi=40, Xi-=40-52.56=-12.56,Ŷi=0.63560+0.01547 × 40=1.2544。
按式(5)~(8)得
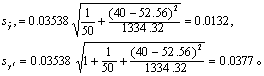
μŶi的95%可信区间为
(1.2544-2.011 × 0.0132,1.2544 +2.011×0.0132)=(1.2279,1.2809)。Yi的95%容许区间为(1.2544-2.011 × 0.0377,1.2544 +2.011 × 0.0377)=(1.1786,1.3302)。
其余横行的计算仿此。
分别将表中第(1)、(5)栏,第(1)、(6)栏;第(1)、(8)栏,第(1)、9)栏数据标在方格坐标纸上,得图中四条曲线。实线范围内为uŶ的95%可信区间,虚线范围内为该地18~25岁女青年体表面积个体值的95%容许区间。
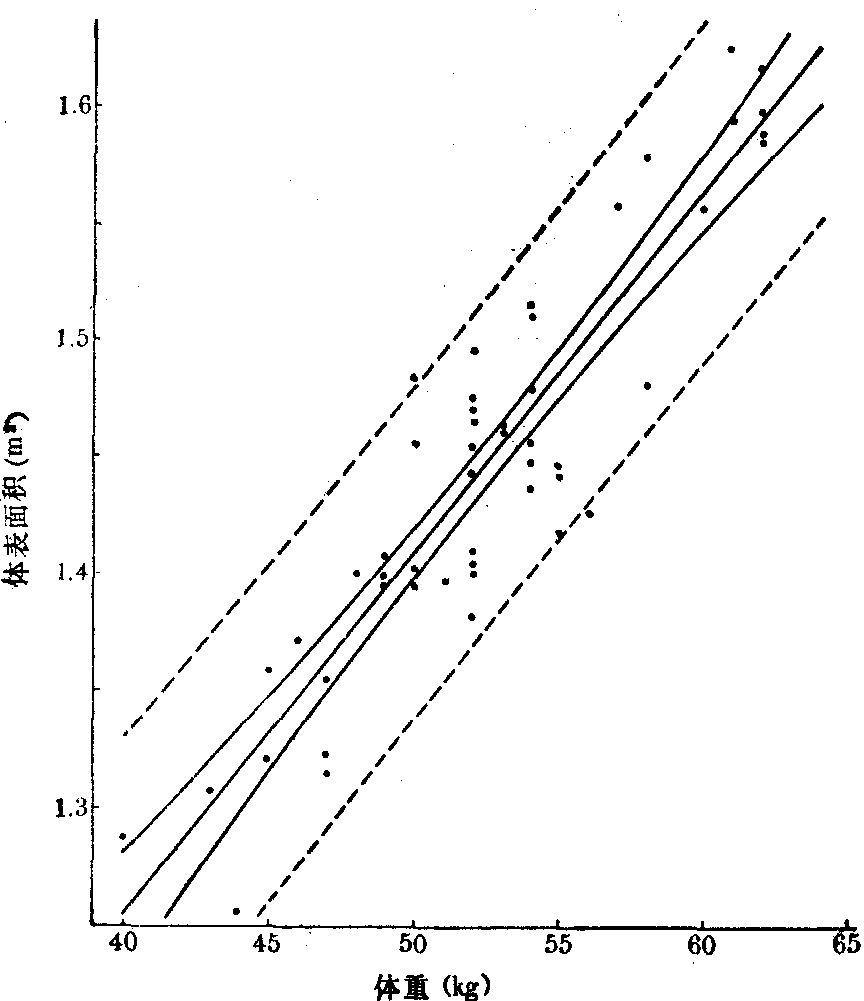
uŶ的95%可信区间与Y的95%容许区间
☚ 直线回归 两直线回归方程比较 ☛
- 纳空春是什么意思
- 纳窝是什么意思
- 纳米是什么意思
- 纳米技术是什么意思
- 纳米旋风是什么意思
- 纳米材料是什么意思
- 纳米比亚是什么意思
- 纳米比亚共和国是什么意思
- 纳米比亚反殖武装斗争是什么意思
- 纳米比亚多党会议是什么意思
- 纳米比亚武装力量是什么意思
- 纳米比亚民族主义之父是什么意思
- 纳米比亚独立是什么意思
- 纳米比亚西南非洲人民组织是什么意思
- 纳米比亚西南非洲民族联盟是什么意思
- 纳米比亚议会是什么意思
- 纳米比亚达马拉委员会是什么意思
- 纳米比亚问题的咨询意见是什么意思
- 纳米民主是什么意思
- 纳米物理与纳米技术是什么意思
- 纳米科学是什么意思
- 纳米科技是什么意思
- 纳米蜂是什么意思
- 纳粟官是什么意思
- 纳粮是什么意思
- 纳粹是什么意思
- 纳粹主义是什么意思
- 纳粹元帅沉浮记是什么意思
- 纳粹党是什么意思
- 纳粹教育的反动性是什么意思
- 纳粹青年党是什么意思
- 纳精器是什么意思
- 纳索是什么意思
- 纳索·威廉·西尼尔是什么意思
- 纳繁于简是什么意思
- 纳繎是什么意思
- 纳繎;𨈓瓤是什么意思
- 纳纱天鹿纹手卷是什么意思
- 纳纳是什么意思
- 纳纳亲是什么意思
- 纳线是什么意思
- 纳细是什么意思
- 纳络酮是什么意思
- 纳绣是什么意思
- 纳绳是什么意思
- 纳维是什么意思
- 纳编是什么意思
- 纳缚僧伽蓝是什么意思
- 纳缚波是什么意思
- 纳缴是什么意思
- 纳罕是什么意思
- 纳罕儿是什么意思
- 纳罗奇之战是什么意思
- 纳罗泼是什么意思
- 纳罪是什么意思
- 纳职是什么意思
- 纳聘是什么意思
- 纳胯妆么是什么意思
- 纳胯挪腰是什么意思
- 纳胯那腰是什么意思