两条异面直线互相垂直

---

如果两条异面直线所成的角是直角，我们就说这两条异面直线互相垂直．

例 空间四边形ABCD，AB=CD=8，M、N、P分别为BD、AC、BC的中点，若异面直线AB和CD成60°的角，求MN的长度．

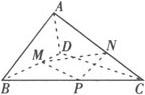
策略 找(或作)出异面直线AB、CD所成的角，然后解三角形即可．

解 分别连结MN，NP，MP．

∵M，P，N分别为BD、AC、BC的中点，

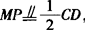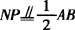∴，，且AB=CD=8．

∴∠MPN(或∠MPN的补角)为AB和CD所成的角，且MP=NP=4．

∴∠MPN=60°或∠MPN=120°．

当∠MPN=60°，由三角形余弦定理可得

MN²=MP²+NP²—2MP·NPcos∠MPN

解得MN=4．

同理，当∠MPN=120°时，，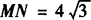

即MN的长为4或．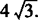

点评 注意解答过程的完整性．