库拉托夫斯基定理kulatuofusiji dingli

图G是平面图的充分必要条件的判定定理.此定理由库拉托夫斯基在1930年给出：图G是平面图当且仅当G不含与K₅或K₃₃在2度结点内同构的子图.有两种操作不影响图G的可平面性. 如图中的左图，在给定图G的边上插入（添加）度数为2的点，即将原来的一条边变为两条边；右图则是将关联于度数为2的点的两条边缩成一条边，即删去2度点.如此，可使下图中左图变为右图.

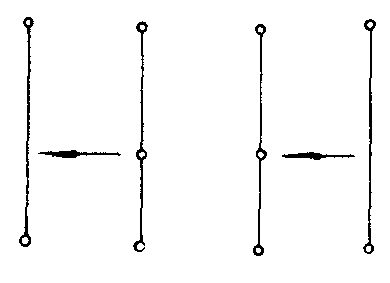
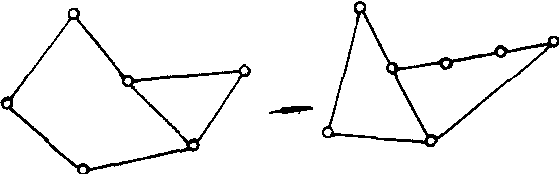
总之，若图G₁,G₂是同构的，或通过反复插入或删去度数为2的点后得到的图G′₁,G₂′是同构的.则称G₁,G₂在2度结点内同构（或同胚）.例如，n≥3,C₃与任何Cn是2度结点内同构的图.
由库拉托夫斯基定理可和，n≥6,K_n是非平面图.因为，K₆删去一点和其关联边后得到的子图是K₅,K₅非平面图，因之，K₆是非平面图，于是，K_n,n≥6都是非平面图.