三角函数式的求值

---

三角函数式求值的三种类型

a．给角求值

b．给值求值

c．给值求角

例1 若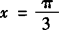是方程2cos(x+α)=1的解α∈(0，2π)，则α=( )．

分析 本题考查了给值求角的问题．

解 依题意可知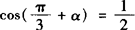2．

由α∈(0，2π)知．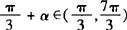

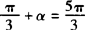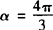观察y=cosx的图象可知即为所求．

例2 sin15°sin30°sin75°的值等于( )．

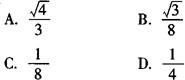
分析 熟悉sin15°与sin75°值的同学可以直接利用

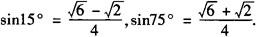
算得结果为1/8，故选C．但是灵活的应用公式巧算则更简捷．

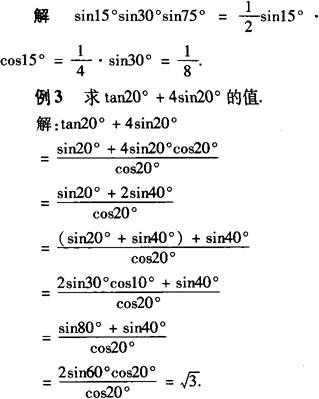
评注 本题上面解法关键有两步，第一步是tan20°化成正、余弦；第二步把2sin40°拆成sin40°+sin40°．

例3 已知tan(α—β)=1/2tanβ=—1/7，且α、β∈(0，π)求2α—β的值．

分析 先找到所求的角与已知函数中的角的联系，再用公式求出所求角的三角函数值，再根据角的范围求出所求角．

解

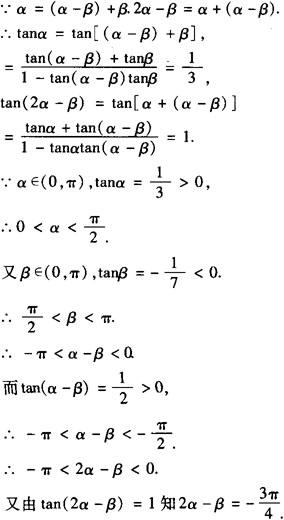
例4 在△ABC中，已知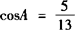，sinB=3/5，求cosC的值

分析 三角形中的三角函数求值问题不能忘了隐形条件，A+B+C=π，A、B、C∈(0，π)．

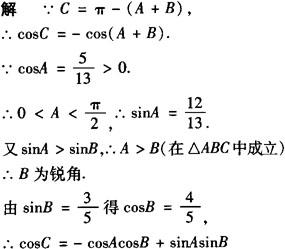
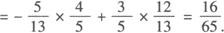
评注 本题如若不弄清B的范围将会产生两个结果．