容斥原理与集合运算Rongchi yuanli yu jihe yunsuan

容斥原理可以通过集合运算给出精确、严格的陈述，而集合运算则可借助集合图得到形象、直观的表现。如图： 三个圆A、B、C, 覆盖的面积等于A、B、C的面积之和，减去A与B, B与C, C与A的公共部分的面积，再加上ABC的公共部分的面积。把A、B、C看作集合， 则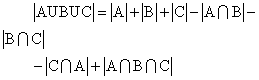
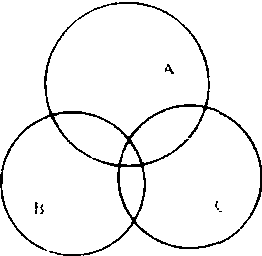
其中|X|表示集合X中的元素个数， 而A∪B∪C表示集合A、B、C的并集，而A∩B∩C表示集合A、B、C的交集。上述结论可以推广到多个集合的情形， 设S₁, …，s_n为n个集合， 则它们的并所含元素个数
|S₁∪S₂∪…∪S_n|=(|S1|+…+|S_n|)-(|S₁∩S₂|++|S₂∩S₃|+…+|s_n∩S₁|)+…+(-1)ⁿ|S₁∩S₂∩…∩Sn|。