多边形

 (斜荡求积)术曰：以少广求之。置中长，乘北阔，半之，为寄。以中长幂减西斜幂，馀为实，以一为隅，开平方，得数，减北阔，馀自乘，并中长幂，共为内率。以小斜幂，并率，减中斜幂，馀半之，自乘于上。以小斜幂乘率，减上，馀，四约之，为实。以一为隅。开平方，得数。加寄，共为荡积。
 

宋·秦九韶《数书九章·田域类》

 【评】秦九韶应用三斜求积方法，给出了四不等边形面积的正确方法。
 《五曹》四不等田东三十五步，西四十五步，南二十五步，北一十五步，问田几何。
 答称三亩八十步，非。实三亩四十步三尺九分六厘八毫七丝半。
 田围四面不等者，必有斜步，然斜步岂可作正步相并？今以一寸代十步为图以证四不等田不可用“东西相并、南北相并，各折半相乘”之法。
 如遇此等田势须分两段取用。
 

宋·杨辉《田亩比类乘除捷法》

 【评】杨辉正确地批评了《五曹》四不等田求法的错误。他提出的分段取用的作法是求不规则图形面积的正确方法。
 今有腰鼓田两头各广八步，中广四步，正从一十二步，问田几何？
 腰鼓田乃梯田二段，上阔相顶。
 《应用算法》:倍中阔作八步，并两阔一十六步，共二十四步，以正从乘得二百八十八步，以四除之。
 鼓田：两头各广四步，中广八步，正从十二步。问田几何？
 鼓田乃梯田二段，下阔相抵。
 《五曹算法》乃并三广，以正从乘而三除，误矣。
 三广田：一头广四步，一头广六步、中广八步，正从一十二步，问田几何？
 倍中阔为十六，并两广十步，共二十六，用长十二乘，得三百一十二，以四除之。
 三广田乃小梯田一段，大梯田一段，下阔相抵。
 或遇此等田势，中阔在正中，可用此术。中阔若偏近一头，只得作两段求，庶不错误。
 

宋·杨辉《田亩比类乘除捷法》

 【评】六世纪甄鸾《五曹算经》提出了“鼓田”、“腰鼓田”的错误公式，杨辉批评了《五曹》的错误，提出了正确的算法，惜未引起重视，《五曹算经》之谬种流传，直至明、清。

多边形duōbiānxíng

同一平面上由三条或三条以上的边构成的图形。

多边形duō biān xíng

由三条或三条以上的边构成的图形。1607年利玛窦译《几何原本》卷一：“在多直线界中之形，为多边形，五边以上俱是。”1885年狄考文译《形学备旨》上卷：“凡形之边数多于四者，俱可以边数命名，如五边形、六边形等等，总名曰多边形。”

多边形duobianxing

由三条或三条以上的线段首尾顺次连结，组成的封闭图形.如图，多边形A₁A₂…A_n.
组成多边形的各条线段叫做多边形的边.如图中的A₁A₂,A₂A₃，…，A_nA₁.
各边的端点叫做多边形的顶点.如图中的A₁,A₂,A₃，…，A_n-1,A_n.
相邻两边所成的角叫做多边形的内角，简称多边形的角.如图中的∠A₁A₂A₃,∠A₂A₃A₄，…，∠A_nA₁A₂.

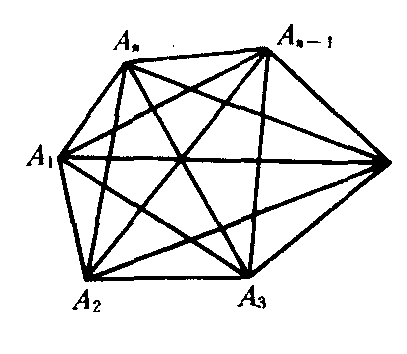
连结多边形不相邻的两个顶点的线段，叫做多边形的对角线.如图中的A₁A₃,A₁A₄，…，A₁A_n-1,A₂A₄….
多边形各边长度的和叫做多边形的周长.如图中多边形A₁A₂A₃……A_n-₁A_n的周长为

A₁A₂+A₂A₃+…+A_n-1A_n+A_nA₁

多边形根据它的边数的多少，可分为三边形（三角形），四边形，五边形，……，n边形(其中n不小于3).

多边形Duobianxing

由三条或三条以上的线段首尾顺次连接，组成的封闭图形。组成多边形的各条线段叫做多边形的边，多边形根据边数的多少，可分为三边形（三角形），四边形，五边形， ……，n边形(其中n不小于3)。多边形每相邻两条线段的端点，叫做多边形的顶点。如图中A,B,C,D,E,F是多边形的顶点。多边形可以用它各个顶点的字母来表示，如图中的这个多边形，记作多边形ABCDEF。连接多边形不相邻的两个顶点的线段， 叫做多边形的对角线。如图中AD就是多边形ABCDEF的一条对角线。多边形相邻两边所组成的角叫做多边形的内角， 简称多边形的角。如图中的∠ABC, ∠BCD, ∠CDE, ∠DE^F, ∠EFA, ∠FAB。多边形各边长度的和叫做多边形的周长， 如图中多边形ABCDEF的周长为AB+BC+CD+DE+EF+AF。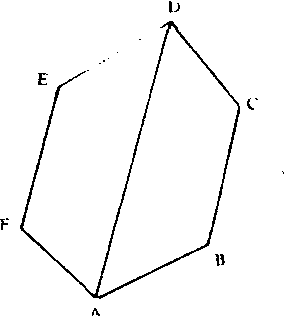

多边形

由3条或者3条以上的线段，首尾顺序连接而成的平面封闭图形。组成多边形的各条线段称为“边”；各边的端点称为“顶点”。

多边形

polygon