伯努利方程
伯努利方程bonuli fangcheng
流体力学的一个基本方程,理想流体做稳定流动时沿某 一流线上任 一点的压强p与速度v之间所满足的方程。即:p/ρ+gh+v2/2=H。式中H为沿流线的常数,h为流线上压强为p速度为v的点相对重力势能参考平面的高度,ρ与g分别为流体的密度和重力加速度。1738年,瑞士数学家、物理学家D·伯努利发表了《流体动力学》一书,首次提出关于理想流体定常流动的伯努利方程。该方程实质上是功能原理在流体力学中的特殊形式,它为流体动力学的创立奠定了基础。在解决具体的流动问题时,可从所选的同一条流线上取两个或三个点列出方程。由于细流管的截面很小,同一截面上各点的压强、速度和高度可近似看作相等。所以方程仍能使用。如果伯努利方程和连续性方程联合使用,则对解决流体问题更加方便。方程中的压强p不是静压强。流动流体内部的压强分布规律与静止流体的不同,只能用伯努利方程求解。对于水平流线,方程式变为p1/ρ+v21/2=p2/ρ+v22/2。它表明,流体内部,流速大的区域压强小,流速小的区域压强大。或者说,流线密集处压强小,流线稀疏处压强大。
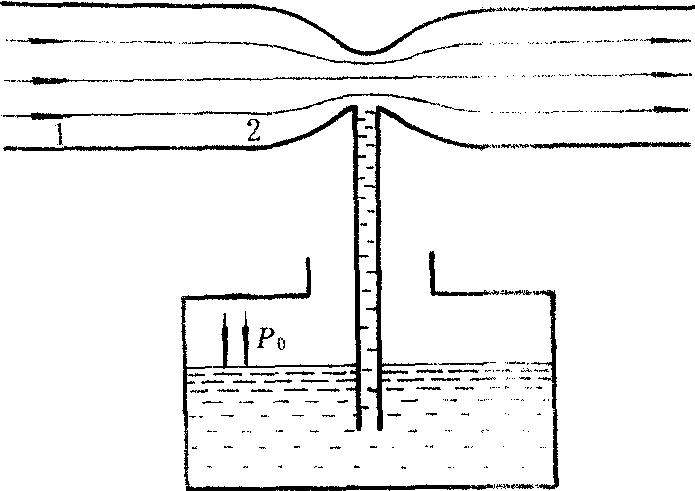
图1
在图1中,2处的流速远大于1处,因此2处的压强比大气压p0小的多,所以容器内的液体在大气压强的作用下被源源不断地输送到2处,这叫做空吸作用。射流真空泵就是利用这种原理工作的。对小孔流速问题,如图2示,方程式变成gh1=v22/2。小孔流速为v2=
 。这意味着小孔流速与自由落体具有相同的速率。由于真实流体内部存在着内摩擦,所以实际的小孔流速要比
。这意味着小孔流速与自由落体具有相同的速率。由于真实流体内部存在着内摩擦,所以实际的小孔流速要比 小(1~2)%。
小(1~2)%。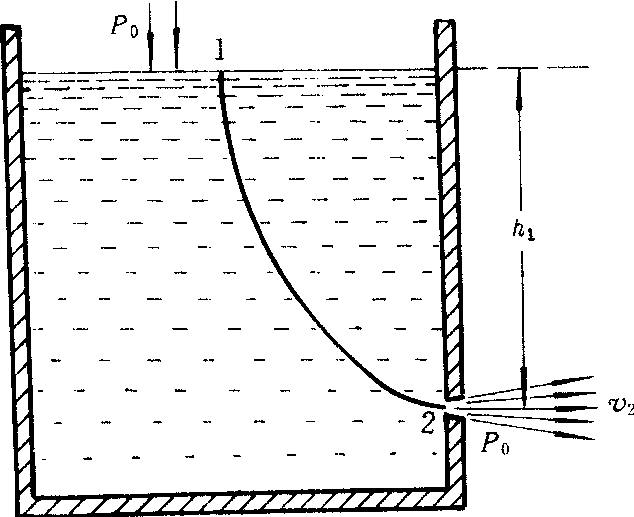
图2
☚ 流体动力学 举力 ☛
伯努利方程
又称“液体的能量方程”。是流体力学中普遍应用的公式。表达式为:
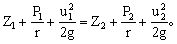
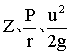 分别为单位位置势能、单位压强势能、单位动能;三项之和即为单位机械能。伯努利方程表明,在理想液体的恒定流动中,同一条流线上各质点的单位机械总能量是守恒的。在理想液体的恒定有势流动中,任一点的单位机械总能量都是相等的。
分别为单位位置势能、单位压强势能、单位动能;三项之和即为单位机械能。伯努利方程表明,在理想液体的恒定流动中,同一条流线上各质点的单位机械总能量是守恒的。在理想液体的恒定有势流动中,任一点的单位机械总能量都是相等的。- 关于理智的名人名言名句大全是什么意思
- 关于理智的名言名句是什么意思
- 关于理智的名言名句大全是什么意思
- 关于理解的名言名句是什么意思
- 关于理论与实践的名人名言名句大全是什么意思
- 关于理论与实践的名言名句是什么意思
- 关于理论的名言名句大全是什么意思
- 关于理财的名言名句是什么意思
- 关于瓦解敌军工作的指示是什么意思
- 关于生与死的名言名句是什么意思
- 关于生产力和生产关系问题是什么意思
- 关于生产力和生产关系问题的论争是什么意思
- 关于生命的名人名言名句大全是什么意思
- 关于生命的名言名句是什么意思
- 关于生命的名言名句大全是什么意思
- 关于生命的起源是什么意思
- 关于生死的名人名言名句大全是什么意思
- 关于生死的名言名句是什么意思
- 关于生死的名言名句大全是什么意思
- 关于生活卷的名言名句是什么意思
- 关于生活的名人名言名句大全是什么意思
- 关于生活的名言名句是什么意思
- 关于生活的名言名句大全是什么意思
- 关于用自由平等口号欺骗人民是什么意思
- 关于申请商标注册要求优先权的暂行规定是什么意思
- 关于申请添购一把铁壶的报告是什么意思
- 关于电影《武训传》的讨论是什么意思
- 关于电影的名人名言名句大全是什么意思
- 关于电影的名言名句是什么意思
- 关于男人与女人的名言名句大全是什么意思
- 关于男人的名人名言名句大全是什么意思
- 关于男人的名言名句是什么意思
- 关于男女的名人名言名句大全是什么意思
- 关于男女的名言名句是什么意思
- 关于番茄汁标准执行问题专家讨论会是什么意思
- 关于疾病的名言名句是什么意思
- 关于痛苦的名人名言名句大全是什么意思
- 关于痛苦的名言名句是什么意思
- 关于痛苦的名言名句大全是什么意思
- 关于登记射人外层空间物体的公约是什么意思
- 关于白居易的文章和故事是什么意思
- 关于监督国际性银行业集团及其跨国分支机构的最低标准的建议是什么意思
- 关于盗伐滥伐森林案件改由公安机关管辖的通知是什么意思
- 关于目前党的政策中的几个重要问题是什么意思
- 关于目前农村工作中若干问题的决定(草案)是什么意思
- 关于目前教育工作的指示是什么意思
- 关于目标的名人名言名句大全是什么意思
- 关于目标的名言名句是什么意思
- 关于目标的名言名句大全是什么意思
- 关于直线的对称变换是什么意思
- 关于直线的对称变换的性质是什么意思
- 关于相猪是什么意思
- 关于省、专区、县三级教育行政工作的几项规定是什么意思
- 关于省、自治区、直辖市可以在1979年设立人民代表大会常务委员会和将革命委员会改为人民政府的决议是什么意思
- 关于真伪的名人名言名句大全是什么意思
- 关于真伪的名言名句是什么意思
- 关于真善美的名言名句大全是什么意思
- 关于真理是什么意思
- 关于真理标准问题的大讨论是什么意思
- 关于真理标准问题的讨论是什么意思