解微分方程
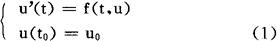
龙格-库塔方法是具有下述形式的一类算法:
Um+1=Um+hφ(tm,um,h),m=0,1,… (2)
其中
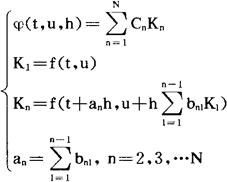
公式中的系数是这样确定的:设u(t)是微分方程(1)的解,将等式u(t+h)-u(t)=hφ(t,u,h)两边在t点展成h的Taylor级数,使左右两端不超过h的q次幂的相应系数相等,就得到了确定系数an,bn1,Cn的方程组。求出它的解,就得到了称为q阶的龙格-库塔方法,它的局部截断误差为0(hq+1)。
常用的三阶龙格-库塔方法是:
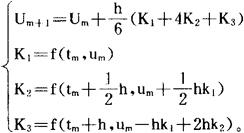
常用的四阶龙格-库塔方法是:
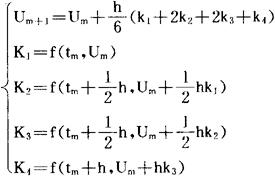
- 库达库尔伯克是什么意思
- 库达苏依列斯乌是什么意思
- 库迈是什么意思
- 库迈之战是什么意思
- 库迈里是什么意思
- 库迪亚人是什么意思
- 库那克萨之战是什么意思
- 库部是什么意思
- 库部主事是什么意思
- 库部令史是什么意思
- 库部司是什么意思
- 库部司员外郎是什么意思
- 库部司郎中是什么意思
- 库部员外郎是什么意思
- 库部尚书郎是什么意思
- 库部承务郎是什么意思
- 库部掌固是什么意思
- 库部曹是什么意思
- 库部曹侍郎是什么意思
- 库部曹郎是什么意思
- 库部曹郎中是什么意思
- 库部郎是什么意思
- 库部郎中是什么意思
- 库都喀是什么意思
- 库都鲁是什么意思
- 库醒头是什么意思
- 库醒饭是什么意思
- 库里亚人是什么意思
- 库里亚大会是什么意思
- 库里人是什么意思
- 库里克塔岛之战是什么意思
- 库里千人是什么意思
- 库里图卡伦是什么意思
- 库里奇亚尔人是什么意思
- 库里昌人是什么意思
- 库里有粮心不慌是什么意思
- 库里申科是什么意思
- 库里申科烈士墓是什么意思
- 库里肖夫是什么意思
- 库里肖夫效应是什么意思
- 库里肖夫,л.в.是什么意思
- 库里让诺夫,л.а.是什么意思
- 库里齐亚人是什么意思
- 库野是什么意思
- 库金是什么意思
- 库钦人是什么意思
- 库钱是什么意思
- 库铁热克沟是什么意思
- 库银是什么意思
- 库锦是什么意思
- 库门是什么意思
- 库门氏是什么意思
- 库阿孜岩画是什么意思
- 库陇勒是什么意思
- 库陇奎鄂拉是什么意思
- 库陇癸之战是什么意思
- 库陇癸山是什么意思
- 库陇癸鄂拉是什么意思
- 库陇葵山是什么意思
- 库院子是什么意思