方差分析

---

对试验数据或观察结果进行分析的一种常用方法，可用来判断各种因素对结果是否有显著影响以及各因素处于何种水平时结果最好。

设x_ij(j=1，2，……q)是由P维正态分布N(μ_i，∑)抽出的大小为q的样本。单因素方差分析的模型为：(1)X_ij=μ+d_i+∑_ij i=1…q(2)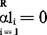，(3)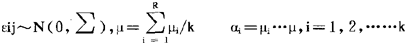，假设A₀：α₁=α₂=α_k的检验如下：令：

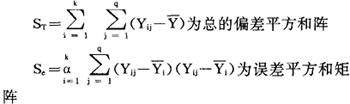
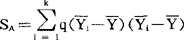为因素A的偏差平方和阵

其中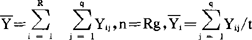

当假设H₀成立时，S_A服从自由度R－1的维希特分布，S_e服从自由度为n－R的维希特分布，而且两者独立，从而可用统计量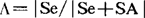遵从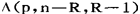分布进行检验。

双因素(A_i，B_j)有交互作用的方差分布模型为：

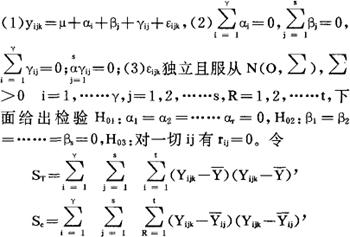
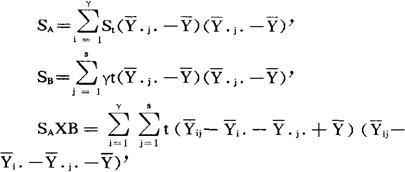
ST=S_e+S_A+S_B+S_AxB

S_e，S_A，S_B，S_AxB分别服从自由度为r_s(t－1)，r－1，s1，(r－1)(s－1)的维希特分布。

在H₀₁成立时，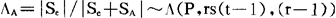

在H₀₂成立时，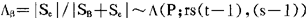

在H₀₃成立时，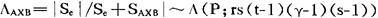

这就是用来检验假设H₀₁，H₀₂，H₀₃的统计量。

上面考虑的方差分析方法是只含有一个因素的问题。多因素方差分析的基本思想与它相似，但要考虑因素之间的交互作用。