反证法

---

1．定义：从命题的结论的反面出发，引出矛盾，从而证明命题的成立，这样的证明方法叫做反证法．

注 从命题的角度看，通过否定结论推出条件不成立，即实际上是证明一个命题的逆否命题．

2．适用题型：反证法属间接证法，当直接证明比较困难时，往往用反证法，如某些结论中含有“至多”、“至少”、“惟一”等词语时往往采用反证法；证明存在性问题，往往采用反证法．

3．反证法证题的一般步骤

❶ 假设命题的结论不成立，即假设结论的反面成立；

❷ 从假设出发，通过推理论证，得出矛盾；

❸ 由矛盾判定假设不成立，从而判定原命题的结论正确．

例1 已知△ABC的三边为a，b，c，∠C=90°，求证：．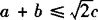

证明 ∵△ABC为直角三角形，且∠C=90°，

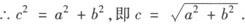
以下用反证法证明．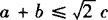

假设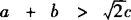，即a+b>，则有

(a+b)²>2(a²+b²)

a²+2ab+b²>2(a²+b²)

a²—2ab+b²<0

(a—b)²<0．

这一结论与(a—b)²≥0是矛盾的．因此，假设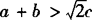是不可能的，所以．

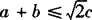例2 求证：两条相交直线有且只有一个交点．

证明 假设结论不成立，则有两条情况：或者没有交点，或者不止一个交点．

(1)如果直线a、b没有交点，那么a∥b，这与已知矛盾；

(2)如果直线a、b不只有一个交点，则至少交于p，p′，这样经过两点p、p′就有两条直线a、b，这与两点确定一条直线矛盾．

由(1)和(2)可知，假设错误，所以，两条相交直线有且只有一个交点．